クレロー型微分方程式

クレロー型微分方程式（Clairaut’s equation） は以下の形式を持つ微分方程式である

\[ y=\frac{dy}{dx}x + f \left( \frac{dy}{dx}\right) \]

ここで関数 \(f\) は\(\frac{dy}{dx}\) の関数である．

クレロー型微分方程式の解法

クレロー型微分方程式の解は関数 \(f\) の形に依存するが，導関数 \(\frac{dy}{dx}\) について解くまでの一般解の導出を行う

まず導関数 \(\frac{dy}{dx}\) を別の関数 \(p\) に置き換える．式は

\[ y=px + f \left(p\right) \]

となる．続いて，上式を\(x\)で微分する．\(y,p\) ともに\(x\)の関数であることに注意すると

\[\begin{split} \begin{aligned} \frac{dy}{dx}&=p+x\frac{dp}{dx} + f'(p) \frac{dp}{dx} \\ p&=p+ \frac{dp}{dx} \left ( x + f'(p)\right ) \\ 0 &= \frac{dp}{dx} \left ( x + f'(p)\right ) \end{aligned} \end{split}\]

となる．第三式が成り立つためには，

\[ \frac{dp}{dx} = \frac{d^2y}{dx^2} = 0 \]

もしくは

\[ x+f'(p)=0 \]

である必要がある．前者の条件は2階微分すると0ということは導関数は定数，つまり

\[ \frac{dy}{dx} = p = C \]

であるため，一般解は

\[ y=Cx+f(C) \]

となる．一方，後者の条件については，以下の方程式より，\(p\)を消去することで \(C\) を含まない特殊解を導出できる．

\[\begin{split} \begin{aligned} &\left\{\begin{array}{l} x = -f'(p) \\ y = px+f(p) \end{array}\right.\\ \end{aligned} \end{split}\]

ただし，関数 \(f\) の形に応じては解を求めることができないので注意されたい．

クレロー型微分方程式の具体例

次の微分方程式を解いてみよう．

\[ y=\frac{dy}{dx}x + \left( \frac{dy}{dx}\right)^2 \]

解答はクリックで確認できる．

この微分方程式は，クレロー型の微分方程式であるので \(p=\frac{dy}{dx}\)として式を変形すると，

\[ y=px + p^2 \]

このとき，\(y\) と \(p\) が \(x\) の関数であることに注意して両辺を \(x\) を微分する．

\[\begin{split} \begin{aligned} \frac{dy}{dx}&=p+x\frac{dp}{dx} + 2p \frac{dp}{dx} \\ p&=p+ \frac{dp}{dx} \left ( x + 2p\right ) \\ 0 &= \frac{dp}{dx} \left ( x + 2p\right ) \end{aligned} \end{split}\]

この等式が成立するためには，

\[ \frac{dp}{dx} = \frac{d^2y}{dx^2} = 0 \]

もしくは

\[ x+2p=0 \]

である必要がある．前者の条件は2階微分すると0ということは導関数は定数，つまり

\[ \frac{dy}{dx} = p = C \]

であるため，一般解は

\[ y=Cx+C^2 \]

となる．後者の条件は，\(p=-x/2\)より，式に代入すると，

\[\begin{split} \begin{aligned} y &= \left ( -\frac{x}{2} \right ) x + \left ( -\frac{x}{2} \right )^2 \\ &= - \frac{1}{4} x^2 \end{aligned} \end{split}\]

という特異解が得られる．

特異解

特異解 とは一般解の任意定数 \(C\) にどのような値を取っても得られない解のことを言う．特殊解は一般解の任意定数を初期条件で固定した解であり，混同しないように注意されたい．

そして，この特異解は得られた曲線に全てに接している曲線である 包絡線 となっている．

包絡線

包絡線（envelope） とは \(\alpha\) をパラメータとする微分可能な関数 \(F(x,y,\alpha)\) が与えられたとき，この関数に接して、かつ接線が軌跡となっている曲線である．ほうらくせんと読む．

Pythonによる実装

では，上記の微分方程式をsympyで解く．ただし，クレロー型であっても微分方程式の形によってはsympyでは計算できない場合があることに注意されたい．

from sympy import symbols, Eq, Derivative, Function, dsolve

# 変数と未知関数の定義
x = symbols('x')
y = Function('y')(x)

# dy/dxの定義
dy = Derivative(y, x)

# 微分方程式の定義
eq = Eq(y, dy*x + dy**2)

# 微分方程式を解く
y_ = dsolve(eq, y)
y_

\[\displaystyle y{\left(x \right)} = \frac{C_{1} \left(C_{1} + 2 x\right)}{4}\]

import numpy as np
from sympy import plotting
import matplotlib.pyplot as plt

N = 10

eqs = []
for c in np.linspace(-1, 1, N):
    eqs.append(y_.rhs.subs(symbols('C1'), c))
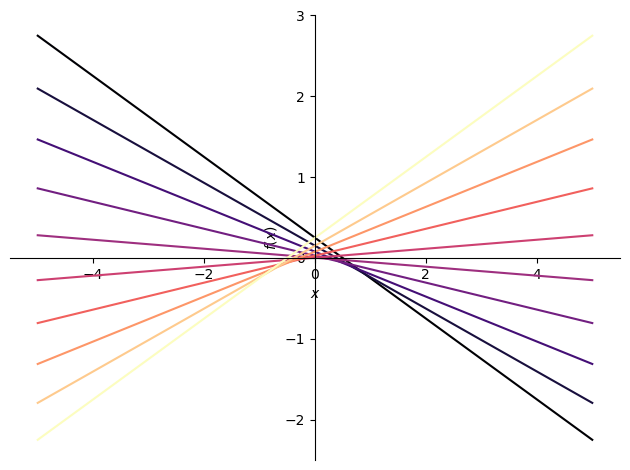
p = plotting.plot(*eqs, (x, -5, 5), show=False)

cm = plt.get_cmap('magma', N)
for i in range(cm.N):
    p[i].line_color = cm(i)
p.show()

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.