フーリエ変換と微分方程式

偏微分方程式

微分方程式には一つの独立変数を持つ未知関数を解く常微分方程式と二つ以上の独立変数を持つ偏微分方程式があった．具体的に，偏微分方程式は関数の偏微分に関する等式であり，以下で与えられた．

\[ \begin{align} F\left(x_1, x_2, ..., x_n, u, \frac{\partial u}{\partial x_1}, \frac{\partial u}{\partial x_2}, ..., \frac{\partial u}{\partial x_n}, \frac{\partial^2 u}{\partial x_1^2}, \frac{\partial^2 u}{\partial x_2^2}, ..., \frac{\partial^2 u}{\partial x_n^2}, ...\right) = 0 \end{align} \]

ここで，\(F\)はある関数，\(x_1, x_2, ..., x_n\)は\(n\)個の独立変数，関数\(u\)は求める未知関数を表し，\(\frac{\partial u}{\partial x_i}\)は\(u\)の\(x_i\)に対する一階の偏微分を表し，\(n\)階の偏微分を含んでた．このような偏微分方程式は一般的に講義で扱った完全微分方程式といった特殊な条件下でないと解くことが難しく，解ける形のものは代表的な偏微分方程式として知られている．ここではその中でも 熱伝導方程式 と呼ばれる偏微分方程式を用いてフーリエ級数展開・フーリエ変換を用いた解法を紹介する．

フーリエ級数展開を用いて熱伝導方程式を解く

熱伝導方程式（Heat Equation） は針金のような均質な物質の長い棒における熱の伝わり方を記述する偏微分方程式である．ここで考えたのは，ある長さ \(l\) の棒（この棒の端を \(0\) とする）について時刻 \(t\) の棒のある位置を\(x\) の熱 \(u(x,t)\) を求める問題である．この熱分布について次の熱伝導方程式（熱伝導方程式）という偏微分方程式が知られている．

\[ \frac{\partial u}{\partial t} = a^2 \frac{\partial^2 u}{\partial x^2}, \quad a > 0 \]

この方程式を棒の端は温度が一定に保たれ（境界条件：\(u(0,t)=u(l,t)=0\)），時刻 \(t=0\) での温度分布は \(f(x)\) である（初期条件：\(u(x,0)=f(x)\)）とする．求めたい関数は熱分布 \(u(x,t)\) であり，位置 \(x\) と時刻 \(t\) における温度の分布の変化を記述するものである．

境界条件

境界条件 とは変数 \(x\) に関して関数の値が指定される条件（特に定義域の端の値）を示す．今回の例では，細い棒の端（\(x=0,l\)）という定義域の端の状態（温度が\(0\)）が境界条件として与えられている．

具体例

では以下の \(u(x,t)\) 熱伝導方程式を解く．ただし，\(0\leq x \leq \pi\) であり，\(t \geq 0\) とする．

\[ \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} \]

境界条件は

\[ u(0,t)=u(\pi,t)=0 \]

であり，初期条件は

\[\begin{split} u(x,0) = \begin{cases}x & 0 \leq x < \frac{\pi}{2} \\ \pi - x & \frac{\pi}{2} \leq x \leq \pi \end{cases} \end{split}\]

となる．

初期条件をプロットしておくと以下となる．

import matplotlib.pyplot as plt
import numpy as np

# 範囲と値を定義
x1 = np.linspace(0, np.pi/2., 100)
y1 = x1
x2 = np.linspace(np.pi/2., np.pi, 100)
y2 = np.pi-x2

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x1, y1, label=r'$y = x \quad 0 < x < \pi/2$', c='b')
plt.plot(x2, y2, label=r'$y = \pi - x \quad \pi/2 < x < \pi$', c='b')

# 軸ラベルとタイトルを追加
plt.xlabel('x')
plt.ylabel('y')

# レジェンドを追加
plt.legend()

# グリッドを追加
plt.grid(True)

# グラフを表示
plt.show()

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

変数分離系の仮定

これを解く．温度分布 \(u(x,t)\) が位置に関する関数 \(p(x)\) と時刻に関する関数 \(q(t)\) から構成されているとし，これらの関数に分離できると仮定する．これを変数分離法の仮定という．

\[ u(x,t) = p(x)q(t) \]

与えられた偏微分方程式の各項の偏導関数を求め

\[ \frac{\partial u}{\partial t} = p(x)q'(t), \quad \frac{\partial^2 u}{\partial x^2} = p''(x)q(t) \]

これらを偏微分方程式に代入すると以下となる．

\[ p(x)q'(t) = p''(x)q(t) \]

これをさらに以下のように変形し，両辺はそれぞれ \(x\) のみの項，\(t\) のみの項になるのでこれらの項は定数となければならない．この定数を \(k\) としておく．

\[ \frac{p''(x)}{p(x)} = \frac{q'(t)}{q(t)} = k \]

以上より，二つの微分方程式が得られる．

\[\begin{split} \begin{align} p''(x) &= kp(x) \\ q'(t) &= kq(t) \end{align} \end{split}\]

これらは解ける形の微分方程式であり，これまでの微分方程式の解法を利用して解く．

位置に関する微分方程式を解く

まず二階線形微分方程式 \(p''(x) = kp(x)\) を解く．これは特性方程式を使って解けばよかったので特性方程式を解く

\[ \lambda^2 - k = 0 \]

この解は \(k\) に応じて変わるので，\(k>0\), \(k=0\), \(k<0\)で場合分けする．

\(k>0\)の場合

まず \(k>0\) のとき，特性方程式の解は \(\lambda = \pm \sqrt{k}\) より，基本解は \(e^{\sqrt{k}x}\)，\(e^{-\sqrt{k}x}\) であり，一般解 \(p(x)=A_1 e^{\sqrt{k}x} + A_2 e^{-\sqrt{k}x}\) が得られる．ここで，任意定数 \(A_1,A_2\) を境界条件（\(u(0,t)=u(\pi,t)=0\)）から求める．代入すると，

\[\begin{split} \begin{align} p(0) &= A_1 e^{\sqrt{k}0} + A_2 e^{-\sqrt{k}0} = A_1 + A_2 = 0 \\ p(\pi) &= A_1 e^{\sqrt{k}\pi} + A_2 e^{-\sqrt{k}\pi} = 0 \\ \end{align} \end{split}\]

この連立方程式の第一式より，\(A_1=-A_2\) が得られ，これを第二式に代入する．

\[ A_1 e^{\sqrt{k}\pi} - A_1 e^{-\sqrt{k}\pi} = A_1 \left (e^{\sqrt{k}\pi} - e^{-\sqrt{k}\pi} \right) = 0 \]

方程式を満たす解は \(A_1 = A_2\) のみであり，このとき \(u(x,t)=0\) となるので \(k>0\) の条件で方程式を満たす解は存在しない．

\(k=0\)の場合

続いて，\(k=0\) のとき，特性方程式の解は \(\lambda = 0\) （重解）が得られ，基本解は \(1,x\) であり，一般解は \(p(x)=A_1 + A_2x\) となる．同様に境界条件を満たす任意定数を求めると，

\[\begin{split} \begin{align} p(0) &= A_1 + A_2 \cdot 0 = A_1 = 0 \\ p(\pi) &= A_1 + A_2 \pi = 0 \\ \end{align} \end{split}\]

となり，\(A_1 = A_2 = 0\) で，境界条件を満たす解は存在しない．

\(k<0\)の場合

最後に，\(k<0\) を考えると，特性方程式の解は \(\lambda = \pm \sqrt{-k} i\) となり，基本解は \(\sin{\sqrt{-k}x}\)，\(\cos{\sqrt{-k}x}\) であり，一般解は \(p(x)=A_1 \sin{\sqrt{-k}x} + A_2 \cos{\sqrt{-k}x}\) が得られる．これまでと同様に境界条件を満たす任意定数を求めると，

\[\begin{split} \begin{align} p(0) &= A_1 \sin{\sqrt{-k}0} + A_2 \cos{\sqrt{-k}0} = A_2 = 0 \\ p(\pi) &= A_1 \sin{\sqrt{-k}\pi} + A_2 \cos{\sqrt{-k}\pi} = 0 \\ \end{align} \end{split}\]

となり，これより，\(A_1 \sin{\sqrt{-k}\pi} = 0\) が得られる．\(A_1\) について，\(A_1=0\) とすると \(u(x,t)=0\) なので \(A_1 \neq 0\) となることが考えられる．\(A_1 \neq 0\) ならば \(\sin{\sqrt{-k}\pi} = 0\) より，これを満たすのは

\[ \sqrt{-k}\pi = n\pi, \quad n=1,2,3,... \]

のときであり，したがって，\(\sqrt{-k} = n, \quad n=1,2,3,...\) となる．以上より，

\[ p(x) = A_n \sin{n\pi}, \quad n=1,2,3... \]

が得られる．ここで \(A_n\) は \(n\) 項目の任意定数である．

時刻に関する微分方程式を解く

続いて，時刻 \(t\) に関する一階線形微分方程式 \(q'(t) = kq(t)\) を考える．前述の結果 \(\sqrt{-k} = n, \quad n=1,2,3,...\) より，微分方程式は

\[ \frac{q'(t)}{q(t)} = -n^2 \]

であることがわかる．変数分離形なので両辺を \(t\) で積分すると，

\[\begin{split} \begin{align} \log |q(t)| &= -n^2 t + B \\ |q(t)| &= e^{-n^2 t + B} \\ q(t) &= \pm e^B e^{-n^2 t} \end{align} \end{split}\]

が得られる．ここで \(B\) は任意定数とする．\(n=1,2,3...\) より \(n\) 項目の \(B\) について \(B_n = \pm e^B\) として置き換えて

\[ q(t) = B_n e^{-n^2 t} \]

が得られた．

特殊解の導出

ここまでで \(u(x,t) = p(x)q(t)\) の変数分離された \(p(x)\)，\(q(t)\) の項の一般解が以下のように得られた．

\[ p(x) = A_n \sin{n\pi}, \quad q(t) = B_n e^{-n^2 t}, \quad n=1,2,3... \]

これを \(u(x,t) = p(x)q(t)\) に代入して整理する．

\[\begin{split} \begin{align} u(x,t) &= A_n \sin{n\pi} B_n e^{-n^2 t} \\ &= C_n e^{-n^2 t} \sin{n\pi} \end{align} \end{split}\]

ただし \(C_n = A_n B_n\) とする．ここから \(C_n\) を求める．まず上記の解は偏微分方程式と境界条件を満たす解なのでその和も解である．

\[ u(x,t) = \sum^{\infty}_{n=1} C_n e^{-n^2 t} \sin{n\pi} \]

これを 重ね合わせの原理 といった（言い換えるとある解と別の解の和，ある解を定数倍した解もまた微分方程式を満たす解となる性質である）．

ここで初期条件

\[\begin{split} u(x,0) = \begin{cases}x & 0 \leq x < \frac{\pi}{2} \\ \pi - x & \frac{\pi}{2} \leq x \leq \pi \end{cases} \end{split}\]

を満たす \(C_n\) を考える．\(t=0\) を代入すると，

\[\begin{split} \begin{align} u(x,0) &= \sum^{\infty}_{n=1} C_n e^{-n^2 \cdot 0} \sin{nx} \\ &= \sum^{\infty}_{n=1} C_n \sin{nx} \\ \end{align} \end{split}\]

となり，これは \(\sin\) 関数のみで表されたフーリエ級数展開である（厳密にはフーリエ正弦級数という）．この関数が \(0 \leq x < \frac{\pi}{2}\) のときは \(x\) で，\(\frac{\pi}{2} \leq x \leq \pi\) のときは \(\pi - x\) となることを考えると，以下のように初期条件を関数 \(f(x)\) としてフーリエ級数展開すれば求めたい \(C_n\) が得られる．ここではフーリエ級数展開は省略するが初期条件 \(f(x)\) のフーリエ級数展開は以下となる．

\[ u(x,0) = \frac{4}{\pi} \left\{ \sin x - \frac{1}{3^2} \sin 3x + \frac{1}{5^2} \sin 5x - \frac{1}{7^2} \sin 7x + \cdots \right\} \]

これを得られた微分方程式の一般解

\[\begin{split} \begin{align} u(x,0) &= \sum^{\infty}_{n=1} C_n \sin{nx} \\ &= C_1 \sin{x} + C_2 \sin{2x} +C_3 \sin{3x} + \cdots \\ \end{align} \end{split}\]

と比較すると項 \(C_n\) が得られる．結果として特殊解は以下となる．

\[ \begin{align} u(x,t) &= \frac{4}{\pi} \left\{ e^{-t} \sin x - \frac{1}{3^2} e^{-3^2 t} \sin 3x + \frac{1}{5^2} e^{-5^2 t}\sin 5x - \frac{1}{7^2} e^{-7^2 t}\sin 7x + \cdots \right\} \end{align} \]

以上より，与えられた熱伝導方程式を解くことができた．

Pythonで特殊解を可視化する

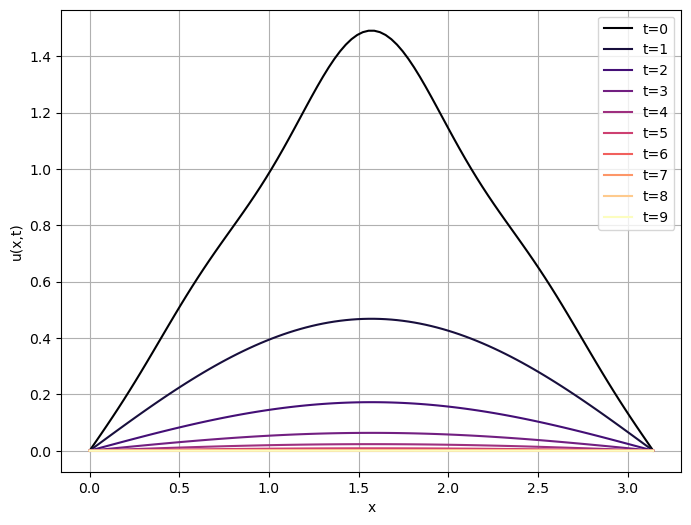
得られた解をpythonでプロットしてみる．ただし \(t=0\) のときは展開する項数が少ないため初期条件と一致しないことに注意されたい．グラフのプロットから次第に温度が低下しているのがわかるかと思う．

import matplotlib.pyplot as plt
import numpy as np

N = 10
cm = plt.get_cmap('magma', N)
plt.figure(figsize=(8, 6))

x = np.linspace(0, np.pi, 100)
for i, t in enumerate(range(10)):
    u = 4./np.pi * (np.exp(-t) * np.sin(x) 
                    - 1./3**2 * np.exp(-3**2*t) * np.sin(3*x) 
                    + 1./5**2 * np.exp(-5**2*t) * np.sin(5*x)
                    - 1./7**2 * np.exp(-7**2*t) * np.sin(7*x))
    plt.plot(x, u, label=f't={t}', c=cm(i))

plt.xlabel('x')
plt.ylabel('u(x,t)')
plt.legend()
plt.grid(True)

フーリエ変換を用いて熱伝導方程式を解く

先ほどの例では長さ \(l\) の棒についてであったが続いて考えるのは無限に長い針金における熱の伝わり方である．フーリエ級数展開を利用した場面や初期条件からもわかるように与えられる初期分布と求めている関数の範囲は空間的な範囲が限られたものであった（言い換えると周期 \(l\) で考えていた）．ここでは無限区間で定義されたフーリエ変換を用いて無限に長い棒での熱伝導方程式を考える．

具体例

先ほどと同様に時刻 \(t\) における位置 \(x\) の温度分布 \(u(x,t)\) を次の偏微分方程式と初期条件から求める．

\[ \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} \]

\[ u(x,0) = \delta(x) \]

変数分離形の仮定

これを解く．前例と同じように温度分布 \(u(x,t)\) が位置に関する関数 \(p(x)\) と時刻に関する関数 \(q(t)\) から構成されているとし，これらの関数に分離できると仮定する．

\[ u(x,t)=p(x)q(t) \]

ここで \(x\) に関するフーリエ変換 \(\mathcal{F}(u(x, t))\) を考える．

\[\begin{split} \begin{align} U(k, t) &=\mathcal{F}(u(x, t)) \\ &=\int_{-\infty}^{\infty} u(x, t) e^{-i k x} d x \\ &=\int_{-\infty}^{\infty} p(x) q(t) e^{-i k x} d x \\ &=q(t) \int_{-\infty}^{\infty} p(x) e^{-i k x} d x \\ &=q(t) P(k) \end{align} \end{split}\]

結果より，温度分布 \(u(x,t)\) のフーリエ変換 \(U(k, t)\) が位置に関する関数 \(p(x)\) をフーリエ変換した結果 \(P(k)\) と時刻に関する関数 \(q(t)\) の積で表現されていることがわかる．

熱伝導方程式をフーリエ変換する

続いて，変数分離形で仮定した \(u(x,t)=p(x)q(t)\) を偏微分方程式に代入することを考える．各偏導関数は

\[\begin{split} \begin{align} \frac{\partial u}{\partial t} &=\frac{\partial}{\partial t}\left \{p(x) q(t) \right \} \\ &=p(x) \frac{d q(t)}{d t} \end{align} \end{split}\]

\[ \frac{\partial^{2} u}{\partial x^{2}}=\frac{d^{2} p(x)}{d x^{2}} q(t) \]

となるので，熱伝導方程式は以下となる．

\[ p(x) \frac{d q(t)}{d t}= \frac{d^{2} p(x)}{d x^{2}} q(t) \]

これを \(x\) についてフーリエ変換すると

\[\begin{split} \begin{align} &\int_{-\infty}^{\infty} p(x) \frac{d q(t)}{d t} e^{-i k x} d x= \int_{-\infty}^{\infty} \frac{d^{2} p(x)}{d x^{2}} q(t) e^{-i k x} d x \\ &\frac{d q(t)}{d t} \int_{-\infty}^{\infty} p(x) e^{-i k x} d x= q(t) \int_{-\infty}^{\infty} \frac{d^{2} p(x)}{d x^{2}} e^{-i k x} d x \end{align} \end{split}\]

が得られる．ここで積分の部分に着目するとフーリエ変換の導関数の性質から両辺をさらに整理できることがわかる．

復習：フーリエ変換の導関数の性質

関数 \(f(t)\) のフーリエ変換 \(\mathcal{F}(f(t))\) と関数 \(f(t)\) の\(n\) 次導関数 \(f^{(n)}(t)\) には以下の関係がある．

\[ \mathcal{F}(f^{(n)}(t)) = (i \omega)^n \mathcal{F}(f(t)) \]

これは導関数 \(f^{(n)}(t)\) のフーリエ変換の結果 \(\mathcal{F}(f^{(n)}(t))\) は元の関数 \(f(t)\) のフーリエ変換後の周波数領域で \(i \omega\) をかけることに等しい．

これより右辺は

\[\begin{split} \begin{align} \int_{-\infty}^{\infty} \frac{d^{2} p(x)}{d x^{2}} e^{-i k x} d x &=(i k)^{2} \mathcal{F}(p(x)) \\ &=(i k)^{2} \int_{-\infty}^{\infty} p(x) e^{-i k x} d x \end{align} \end{split}\]

となり，熱伝導方程式をフーリエ変換した式は以下のように書ける．

\[ \begin{align} \frac{d q(t)}{d t} \int_{-\infty}^{\infty} p(x) e^{-i k x} d x= q(t)(i k)^{2} \int_{-\infty}^{\infty} p(x) e^{-i k x} d x \end{align} \]

積分を消去すると

\[ \frac{d q(t)}{d t}= q(t)(i k)^{2}=-k^{2} q(t) \]

という微分方程式が得られ，\(q(t)\)について解くと以下となる．

\[ q(t)=C e^{- k^{2} t} \]

ただし \(C\) は積分定数とする．再び \(u(x,t)\) のフーリエ変換 \(U(x,t)\) に戻り \(q(t)\) を代入する．

\[\begin{split} \begin{align} U(k, t) &=q(t) \times P(k) \\ &=P(k) \times C e^{- k^{2} t} \end{align} \end{split}\]

特殊解の導出

これを逆フーリエ変換すれば \(u(x,t)\) が得られるが，初期条件 \(u(x,0) = \delta(x)\) があるので先にフーリエ変換後で特殊解を求める．

\[\begin{split} \begin{align} U(x, 0) &=P(k) \times C e^{- k^{2} \cdot 0} \\ &=C P(k) \\ \end{align} \end{split}\]

\[\begin{split} \begin{align} U(x, 0) &=\int_{-\infty}^{\infty} u(x, 0) e^{-i k x} d x \\ &=\int_{-\infty}^{\infty} \delta(x) e^{-i k x} d x \\ &=\int_{-\infty}^{\infty} \delta(x) e^{-i k x} d x \\ &=e^{-i k \times 0} \\ &=1 \end{align} \end{split}\]

ただし，5行目はデルタ関数の性質 \(\int_{-\infty}^{\infty} g(t) \delta(t) d t=g(0)\) を利用している． これより，\(C P(k) = 1\) となり，\(U(k, t)=P(k) \times C e^{- k^{2} t}\) に代入すると

\[ U(k, t)=e^{- k^{2} t} \]

が得られる．

逆フーリエ変換より特殊解を求める

これを逆フーリエ変換して \(u(x,t)\) を求めたい．

\[\begin{split} \begin{align} u(x, t) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} U(k, t) e^{i k x} d k \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{-k^{2} t} e^{i k x} d k \\ \end{align} \end{split}\]

この積分計算であるがガウス関数のフーリエ変換を利用する．

ガウス関数のフーリエ変換

\(f(t) = e^{-at^2},\quad a >0\) のフーリエ変換は以下で与えられる．

\[\begin{split} \begin{align} &\frac{1}{2 \pi} \int_{-\infty}^{\infty} \sqrt{\frac{\pi}{a}} e^{-\frac{k^{2}}{4 a}} e^{i k x} d k=e^{-a x^{2}} \\ &\int_{-\infty}^{\infty} e^{-\frac{k^{2}}{4 a}} e^{i k x} d k=2 \pi \sqrt{\frac{a}{\pi}} e^{-a x^{2}} \end{align} \end{split}\]

このガウス関数に関する積分を利用するために \(a=1\) で \(k=\frac{\omega}{2\sqrt{t}}\) として変数変換する．

\[\begin{split} \begin{align} u(x, t) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{-k^{2} t} e^{i k x} d k \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{-\left(\frac{\omega}{2 \sqrt{t}}\right)^{2} t} e^{i\left(\frac{\omega}{2\sqrt{t}}\right) x} \frac{1}{2\sqrt{t}} d \omega \\ &=\frac{1}{2 \pi} \cdot \frac{1}{2 \sqrt{t}} \int_{-\infty}^{\infty} e^{- \frac{\omega^{2}}{4t} \cdot t} e^{i \frac{\omega}{2 \sqrt{t}} x} d \omega \\ &=\frac{1}{2 \pi} \cdot \frac{1}{2 \sqrt{t}} \int_{-\infty}^{\infty} e^{-\frac{\omega^{2}}{4}} \cdot e^{i \frac{x}{2 \sqrt{t}}\omega} d \omega\\ &=\frac{1}{4 \pi \sqrt{t}} \int_{-\infty}^{\infty} e^{-\frac{\omega^{2}}{4}} \cdot e^{i \frac{x}{2 \sqrt{t}} \omega} d \omega\\ &=\frac{1}{4 \pi \sqrt{t}} \cdot 2 \pi \sqrt{\frac{1}{\pi}} e^{- \left(\frac{x}{2 \sqrt{t}}\right)^{2}}\\ &=\frac{1}{2 \sqrt{t}} \cdot \sqrt{\frac{1}{\pi}} e^{- \frac{x^{2}}{4 t}}\\ &=\frac{1}{2 \sqrt{\pi t}} e^{-\frac{x^{2}}{4 t}} \end{align} \end{split}\]

以上より与えられた熱伝導方程式の解が得られた．

Pythonで特殊解を可視化する

得られた解 \(u(x,t)=\frac{1}{2 \sqrt{\pi t}} e^{-\frac{x^{2}}{4 t}}\) をpythonでプロットしてみる．時刻が進むにつれて温度分布が低下していることがわかるかと思う．

import numpy as np
import matplotlib.pyplot as plt

r = 1.5
x = np.linspace(-r, r, 100)
t = np.linspace(1e-14, 1, 100)
xx, tt = np.meshgrid(x, t)

h = 1 / (2 * np.sqrt(np.pi * tt))
h = h * np.exp(- xx**2 / (4 * tt))

plt.imshow(h, cmap='magma')
plt.axis('off')

(-0.5, 99.5, 99.5, -0.5)