同次微分方程式

同次微分方程式 とは，微分方程式の関数 \(f(x,y)\) が\(f(\frac{y}{x})\)であるとき，つまり，以下のような形式の微分方程式のことを示す．

\[ \begin{align} \frac{dy}{dx} = f\left(\frac{y}{x}\right) \end{align} \]

この一般解は以下で与えられる．

\[ \begin{align} \int \frac{1}{f(u) -u}du= \log | x | + C \end{align} \]

ただし，\(C\)は積分定数とする．

一般解の導出

同次微分方程式をを解くためには，\(\frac{y}{x}=u\)として変数変換をすれば良い．この変数変換は

\[ \begin{align} \frac{y}{x}=u \Rightarrow y = xu \end{align} \]

であり，これを\(x\)について微分すると，

\[ \begin{align} \frac{dy}{dx} = u + x\frac{du}{dx} \end{align} \]

のようになる．ここで \(u=y/x\) という \(x\) の関数なので右辺は積の微分を利用する．そして，\(u\)について整理すると，

\[ \begin{align} \frac{du}{dx} = \frac{1}{x} \left(\frac{dy}{dx} -u\right) \end{align} \]

となり，\(\frac{dy}{dx}=f\left(\frac{y}{x}\right)=f(u)\)であるので，次の形になる．

\[ \begin{align} \frac{du}{dx} = \frac{1}{x} \left(f(u) -u\right) \end{align} \]

上記の式は \(u\) と \(x\) のみが含まれ，\(u\) と \(x\) について以下のように整理すると変数分離形となる．

\[ \begin{align} \frac{1}{f(u) -u}du= \frac{1}{x} dx \end{align} \]

変数分離形の解法と同様に両辺を積分し，

\[ \begin{align} \int \frac{1}{f(u) -u}du= \int \frac{1}{x} dx \end{align} \]

以下の一般解が得られる．

\[ \begin{align} \int \frac{1}{f(u) -u}du= \log | x | + C \end{align} \]

ただし，\(C\)は積分定数とする．

積の微分法則

積の微分法則とは \(y=f(x)g(x)\) という関数の変数\(x\) の微分は以下となる法則である．

\[ \frac{dy}{dx} = f'(x)g(x) + f(x)g'(x) \]

\(u\) の変数変換では，\(u\) は \(x\) の関数であるので，\(y'=u'x + ux'\) という微分になっていることに注意されたい．

同次微分方程式の具体例

では，次の同次微分方程式を解いてみよう．

\[ \frac{dy}{dx} = \frac{x^2 + y^2}{xy} \]

解答はクリックで確認できる．

一見すると変数分離形とも同次形とも見て取れないが，ここで，右辺を \(x^2\) で割ると以下のように \(y/x\) の形が現れる．

\[ \frac{dy}{dx} = \frac{1 + \left(\frac{y}{x}\right)^2}{\left(\frac{y}{x}\right)} \]

ここで \(u=\frac{y}{x}\) として変数変換をする．前述より，

\[ \begin{align} u + x\frac{du}{dx} &= \frac{1 + u^2}{u} \end{align} \]

であり，変数変換をした \(y\) の導関数を \(\frac{dy}{dx} = \frac{1 + u^2}{u}\) を代入すると

\[\begin{split} \begin{align} \frac{dy}{dx} &= u + x\frac{du}{dx} \\ u + x\frac{du}{dx} &= \frac{1 + u^2}{u} \\ x\frac{du}{dx} &= \frac{1 + u^2}{u} - u \\ x\frac{du}{dx} &= \frac{1}{u} \\ u du &= \frac{1}{x} dx \end{align} \end{split}\]

と変数分離形となった．変数分離形の解法にしたがって両辺を積分する．

\[\begin{split} \begin{align} \int u du &= \int \frac{1}{x} dx \\ \frac{u^2}{2} &= \log |x| + D \\ u^2 &= 2 \log |x| + 2D \\ \end{align} \end{split}\]

最後に，\(u=\frac{y}{x}\) を代入し，\(y\) について整理すると，

\[\begin{split} \begin{align} \frac{y^2}{x^2} &= 2 \log |x| + 2D \\ y^2 &= 2 x^2 \log |x| + 2D x^2 \\ y &= \pm x \sqrt{2 \log |x| + C} \end{align} \end{split}\]

として，一般解が得られる．ここで，\(D\)は積分定数であり，\(C=2D\)とした．

Pythonによる実装

では，これをsympyで解く．

from sympy import symbols, Eq, Derivative, Function, dsolve

# 変数，関数，導関数を定義．
x = symbols('x')
y = Function('y')(x)
dy = Derivative(y, x)

# 与えられた同次微分方程式を定義
eq = Eq(dy, (x**2 + y**2) / (x*y))

# 微分方程式を解く．
y_ = dsolve(eq, y)

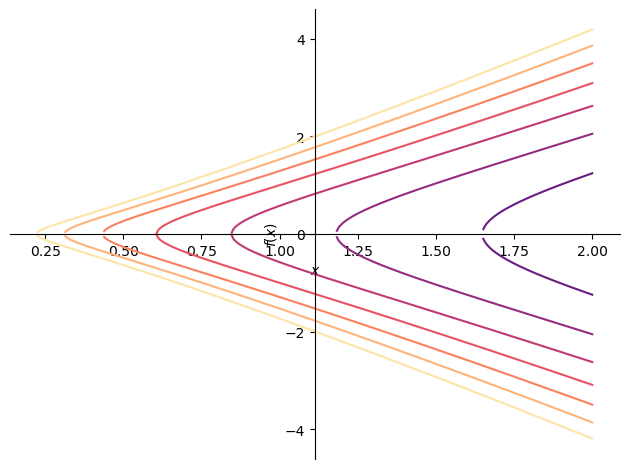
このとき手計算した一般解からもわかるように \(y\) は二つの一般解を持つことに注意する．

y_[0]

\[\displaystyle y{\left(x \right)} = - x \sqrt{C_{1} + 2 \log{\left(x \right)}}\]

y_[1]

\[\displaystyle y{\left(x \right)} = x \sqrt{C_{1} + 2 \log{\left(x \right)}}\]

import numpy as np
from sympy import plotting
import matplotlib.pyplot as plt

N = 10

eqs = []
for c in np.linspace(-3, 3, N):
    eqs.append(y_[0].rhs.subs(symbols('C1'), c))
    eqs.append(y_[1].rhs.subs(symbols('C1'), c))
p = plotting.plot(*eqs, (x, -2, 2), show=False)

cm = plt.get_cmap('magma', N*2)
for i in range(0, cm.N, 2):
    p[i].line_color = cm(i)
    p[i+1].line_color = cm(i)
p.show()

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.