フーリエ級数展開

フーリエ係数

フーリエ級数展開は関数 \(f(x)\) を \(\sin\)関数と\(\cos\)関数の足し合わせで近似する方法であり，以下で与えられる．

\[ \begin{align} f(x) \sim a_0 + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \end{align} \]

ここで，\(a_0, a_n, b_n\)は以下で与えられる．

\[\begin{split} \begin{align} a_{0}&=\frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx \\ a_{n}&=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx \quad(n=1,2,3 \cdots) \\ b_{n}&=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x d x \quad(n=1,2,3 \cdots) \end{align} \end{split}\]

フーリエ級数展開が係数 \(c\) と関数 \(\phi\) の線型結合からなる足し合わせで関数を近似していることを最小二乗法からイメージできるかと思う．そして，関数 \(\phi\) の設計を\(\sin\)関数と\(\cos\)関数からなる 三角関数系 から設計することでフーリエ級数展開の第一式となることを理解してもらったはずだ．本講義では，三角関数系の直交性の性質を確認し，係数 \(c\) である フーリエ係数 \(a_0, a_n, b_n\) の導出を試みる．

三角関数系

では，フーリエ級数展開のフーリエ級数を三角関数の直交性から導出する．そのために，三角関数系

\[ \left \{1, \cos x, \sin x, \cos 2x, \sin 2x,\ldots \right \} \]

は区間 \([-\pi, \pi]\) で直交するという性質をまず確認する．

おさらいであるが関数の直交と直交関数系について復習したい．

関数の直交と直交関数系

区間 \([a,b]\) 上の関数 \(f(x), g(x)\) は以下のとき直交する．

\[ \int_{a}^{b}\ f(x) g(x) dx= 0 \]

そして，関数の集合 \(\{\phi_i(x)\}^n_{i=0}\) が互いに直交するとき，区間 \([a,b]\) 上の直交関数系であるという．

三角関数系 \(1, \cos kx, \sin kx, k=1,2,3,\ldots,\) が区間 \([-\pi, \pi]\) 上で直交関数系であることを示すためにすべての関数の組み合わせで積分し互いに異なる関数同士のときに積分結果が \(0\) となることをを確認する．

• \(1\) と \(\cos kx\) の組み合わせ

  \[ \int_{-\pi}^{\pi}\ 1 \cdot \cos kx dx = 0 \]

• \(1\) と \(\sin kx\) の組み合わせ

  \[ \int_{-\pi}^{\pi}\ 1 \cdot \sin kx dx = 0 \]

• \(\cos kx\) と \(\sin lx\) の組み合わせ

  \[\begin{split} \begin{align} \int_{-\pi}^{\pi} \cos kx \sin lx dx &= \int_{-\pi}^{\pi} \frac{1}{2} \left \{ \sin \left ( k+l \right ) x - \sin \left ( k - l \right ) x \right \} dx \\ &=\frac{1}{2} \int_{-\pi}^{\pi} \sin \left ( k+l \right ) x dx - \frac{1}{2} \int_{-\pi}^{\pi} \sin \left ( k - l \right ) x dx \\ &=0 \end{align} \end{split}\]

• \(k \neq l\) のときの \(\cos kx\) と \(\cos lx\) の組み合わせ

  \[\begin{split} \begin{align} \int_{-\pi}^{\pi} \cos kx \cos lx dx &= \int_{-\pi}^{\pi} \frac{1}{2} \{ \cos \left ( k+l \right ) x + \cos \left ( k - l \right ) x \} dx \\ &=\frac{1}{2} \int_{-\pi}^{\pi} \cos \left ( k+l \right ) x dx + \frac{1}{2} \int_{-\pi}^{\pi} \cos \left ( k - l \right ) x dx \\ &=0 \end{align} \end{split}\]

• \(k \neq l\) のときの \(\sin kx\) と \(\sin lx\) の組み合わせ

  \[\begin{split} \begin{align} \int_{-\pi}^{\pi} \sin kx \sin lx dx &= \int_{-\pi}^{\pi} \frac{1}{2} \{ \cos \left ( k+l \right ) x - \cos \left ( k - l \right ) x \} dx \\ &=\frac{1}{2} \int_{-\pi}^{\pi} \cos \left ( k+l \right ) x dx - \frac{1}{2} \int_{-\pi}^{\pi} \cos \left ( k - l \right ) x dx \\ &=0 \end{align} \end{split}\]

• \(1\) と \(1\) の組み合わせ

  \[ \int_{-\pi}^{\pi}\ 1^2 dx = 2\pi \]

• \(k = l\) のときの \(\cos kx\) と \(\cos lx\) の組み合わせ

  \[\begin{split} \begin{align} \int_{-\pi}^{\pi} \cos kx \cos lx dx &= \int_{-\pi}^{\pi} \cos^2 kx dx \\ &= \int_{-\pi}^{\pi} \frac{1}{2} \left ( 1 + \cos 2kx \right ) dx = \pi \end{align} \end{split}\]

• \(k = l\) のときの \(\sin kx\) と \(\sin lx\) の組み合わせ

  \[\begin{split} \begin{align} \int_{-\pi}^{\pi} \sin kx \sin lx dx &= \int_{-\pi}^{\pi} \sin^2 kx dx \\ &= \int_{-\pi}^{\pi} \frac{1}{2} \left ( 1 - \cos 2kx \right ) dx = \pi \end{align} \end{split}\]

以上の積分計算から三角関数系 \(\{1, \cos kx, \sin kx\}, k=1,2,3,\ldots,\) が区間 \([-\pi, \pi]\) 上で直交関数系であることがわかった．

フーリエ係数の導出

ここでは，フーリエ級数展開のフーリエ級数について (1) 関数の最小二乗法 と (2) 三角関数系の直交性 の二通りの導出を紹介する．

関数の最小二乗法からの導出

まず (1) 関数の最小二乗法について，具体的には，関数の最小二乗法で導出した \(c_i\) を計算すると導出できる．簡単に復習すると，区間 \([a,b]\) において，任意の関数 \(f(x)\) を直交する \(n\) 個の関数 \(\{ \phi_i(x) \}^n_{i=1}\) の線形結合

\[\begin{split} \begin{align} f(x) &\approx \sum_{k=1}^{n} c_{k} \phi_{k}(x)\\ &=c_1 \phi_{1}(x)+c_2 \phi_{2}(x) + \cdots c_n \phi_n(x) \end{align} \end{split}\]

で表現し，区間 \([a,b]\) 上のすべての点 \(x\) で均一に近似するように次の最小化問題を考えることで関数の近似を最小二乗法から行うことができた．さらに直交関数系で設計した \(\phi\) の性質より正規方程式の導出から係数 \(c_i\) は以下の形でシンプルに書くことができた．

\[ c_i = \frac{\int_{a}^{b} \phi_{i} \left ( x \right ) f \left ( x \right) dx }{\int_{a}^{b} \phi_{i} \left ( x \right )^2 dx }, \qquad i=1,...,n \]

この式をもとに，\(a_0, a_k, b_k\) を導出する．まず，\(a_0\) について，対応する \(\phi_0\) は \(1\) であることに注意して計算すると

\[\begin{split} \begin{align} a_0 = c_0 &= \frac{\int_{-\pi}^{\pi} 1 \cdot f(x) dx}{\int_{-\pi}^{\pi} 1^2 dx} \\ &= \frac{\int_{-\pi}^{\pi} f(x) dx}{2\pi} \\ &= \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) dx \\ \end{align} \end{split}\]

となる．続いて，\(\cos\)関数の場合の \(k\) 項である \(a_k\) を導出する．

\[\begin{split} \begin{align} a_k = c_k &= \frac{\int_{-\pi}^{\pi} \cos kx f(x) dx}{\int_{-\pi}^{\pi} \cos^2 kx dx} \\ &= \frac{\int_{-\pi}^{\pi} f(x) \cos kx dx}{\pi} \\ &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos kx dx \\ \end{align} \end{split}\]

同様にして，\(\sin\)関数の場合の \(k\) 項である \(b_k\) を導出する．

\[\begin{split} \begin{align} a_k = c_k &= \frac{\int_{-\pi}^{\pi} \sin kx f(x) dx}{\int_{-\pi}^{\pi} \sin^2 kx dx} \\ &= \frac{\int_{-\pi}^{\pi} f(x) \sin kx dx}{\pi} \\ &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin kx dx \\ \end{align} \end{split}\]

以上より，フーリエ級数展開のフーリエ級数を (1) 関数の最小二乗法 から導出できた．

三角関数系の直交性からの導出

続いて，(2) 三角関数系の直交性 からの導出について線形結合の式

\[ f(x) = a_{0} + a_{1} \cos x + b_{1} \sin x + a_{2} \cos 2x + b_{2} \sin 2x + \cdots \]

からスタートして，自身以外との関数の内積が \(0\) となるという直交関数系の性質を活用することを考える．

まず \(a_0\) の導出は上記の線型結合の式の両辺に \(1\) をかけて両辺を区間 \([-\pi, \pi]\) で積分することで導出できる．

\[\begin{split} \begin{align} \int_{-\pi}^{\pi} 1 \cdot f(x) dx &= \int_{-\pi}^{\pi} 1 \cdot \left \{ a_{0} + a_{1} \cos x + b_{1} \sin x + a_{2} \cos 2x + b_{2} \sin 2x + \cdots \right \} dx \\ &= a_0 \int_{-\pi}^{\pi} 1 dx+ a_1 \int_{-\pi}^{\pi} \cos x dx + b_1 \int_{-\pi}^{\pi} \sin x dx \\ & \quad + a_2 \int_{-\pi}^{\pi} \cos 2x dx + b_2 \int_{-\pi}^{\pi} \sin 2x dx + \cdots \\ &= 2 a_0 \pi \\ a_0 &= \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx \end{align} \end{split}\]

続いて，\(a_k\) の導出は上記の線型結合の式の両辺に \(\cos kx\) をかけて両辺を区間 \([-\pi, \pi]\) で積分することで導出できる．

\[\begin{split} \begin{align} \int_{-\pi}^{\pi} f(x) \cos kx dx &= \int_{-\pi}^{\pi} \cos kx \left \{ a_{0} + a_{1} \cos x + b_{1} \sin x + a_{2} \cos 2x + b_{2} \sin 2x + \cdots \right \} dx \\ &= a_0 \int_{-\pi}^{\pi} \cos kx dx+ a_1 \int_{-\pi}^{\pi} \cos x \cos kx dx + b_1 \int_{-\pi}^{\pi} \sin x \cos kx dx \\ & \quad + a_2 \int_{-\pi}^{\pi} \cos 2x \cos kx dx + b_2 \int_{-\pi}^{\pi} \sin 2x \cos kx dx + \cdots \\ & \qquad + a_k \int_{-\pi}^{\pi} \cos kx \cos kx dx + b_k \int_{-\pi}^{\pi} \sin kx \cos kx dx + \cdots \\ &= a_k \int_{-\pi}^{\pi} \cos^2 kx dx \\ &= a_k \int_{-\pi}^{\pi}\ \frac{1}{2} \left ( 1 + \cos 2kx \right ) dx \\ &= a_k \pi \\ a_k &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos kx dx \end{align} \end{split}\]

最後に，\(b_k\) の導出は上記の線型結合の式の両辺に \(\sin kx\) をかけて両辺を区間 \([-\pi, \pi]\) で積分することで導出できる．

\[\begin{split} \begin{align} \int_{-\pi}^{\pi} f(x) \sin kx dx &= \int_{-\pi}^{\pi} \sin kx \left \{ a_{0} + a_{1} \cos x + b_{1} \sin x + a_{2} \cos 2x + b_{2} \sin 2x + \cdots \right \} dx \\ &= a_0 \int_{-\pi}^{\pi} \sin kx dx+ a_1 \int_{-\pi}^{\pi}\ \cos x \sin kx dx + b_1 \int_{-\pi}^{\pi}\ \sin x \sin kx dx \\ & \quad + a_2 \int_{-\pi}^{\pi} \cos 2x \sin kx dx + b_2 \int_{-\pi}^{\pi} \sin 2x \sin kx dx + \cdots \\ & \qquad + a_k \int_{-\pi}^{\pi} \cos kx \sin kx dx + b_k \int_{-\pi}^{\pi} \sin kx \sin kx dx + \cdots \\ &= b_k \int_{-\pi}^{\pi} \sin^2 kx dx \\ &= b_k \int_{-\pi}^{\pi}\ \frac{1}{2} \left ( 1 - \cos 2kx \right ) dx \\ &= b_k \pi \\ b_k &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin kx dx \end{align} \end{split}\]

以上より，フーリエ級数展開のフーリエ級数を (2) 三角関数系の直交性 から導出できた．

具体例

では，区間 \([-\pi, \pi]\) 上の以下の関数 \(f(t)\) についてフーリエ級数展開してみよう．

\[\begin{split} f(t) = \begin{cases} 1 & -\pi < t \leq 0 \\ 0 & 0 < t \leq \pi \end{cases} \end{split}\]

解答はクリックで確認できる．

フーリエ係数 \(a_0, a_k, b_k\) を順に計算する．まずフーリエ係数 \(a_0\) を上記で導出したフーリエ係数の式から計算する．

\[\begin{split} \begin{align} a_0 &= \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx \\ &= \frac{1}{2 \pi} \left\{ \int_{-\pi}^{0} 1 dt + \int_{0}^{\pi} 0 dt \right\} \\ &= \frac{1}{2 \pi} \left [ t \right ]^{0}_{-\pi} \\ &= \frac{1}{2 \pi} \left \{ 0 + \pi \right \} = \frac{1}{2} \end{align} \end{split}\]

続いて，フーリエ係数 \(a_k\) は以下のように計算できる．

\[\begin{split} \begin{align} a_k &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos kx dx \\ &= \frac{1}{\pi} \left\{ \int_{-\pi}^{0} 1 \cdot \cos kx dx + \int_{0}^{\pi} 0 \cdot \cos kx dx \right\} \\ &= \frac{1}{\pi} \left [ \frac{1}{k} \sin kx \right ]^{0}_{\pi} \\ &= \frac{1}{\pi} \left \{ \frac{1}{k} \sin 0 - \frac{1}{k} \sin \left ( -k \pi \right ) \right \} \\ &= \frac{1}{k\pi} \sin k\pi = 0 \end{align} \end{split}\]

最後に，フーリエ係数 \(b_k\) は以下のように計算できる．

\[\begin{split} \begin{align} b_k &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin kx dx \\ &= \frac{1}{\pi} \left\{ \int_{-\pi}^{0} 1 \cdot \sin kx dx + \int_{0}^{\pi} 0 \cdot \sin kx dx \right\} \\ &= \frac{1}{\pi} \left [ - \frac{1}{k} \cos kx \right ]^{0}_{\pi} \\ &= \frac{1}{\pi} \left \{ - \frac{1}{k} \cos 0 + \frac{1}{k} \cos \left ( -k \pi \right ) \right \} \\ &= - \frac{1}{k \pi} \left (1 - \cos k \pi \right ) \\ &= - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \\ \end{align} \end{split}\]

以上より，フーリエ係数が以下のように計算された．

\[ \begin{align} a_0 = 1, \quad a_k = 0, \quad b_k = - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \end{align} \]

これをフーリエ級数展開の式に代入する．

\[\begin{split} \begin{align} f(t) &\approx a_0 + \sum_{n=1}^{\infty} (a_k \cos kx + b_k \sin kx) \\ &= \frac{1}{2} + \sum_{k=1}^{\infty} \left [0 \cdot \cos kx - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \sin kx \right] \\ &= \frac{1}{2} - \frac{1}{\pi} \sum_{k=1}^{\infty} \left [ \frac{\left \{1 - \left ( -1 \right )^k \right \}}{k} \sin kx \right] \\ &= \frac{1}{2} - \frac{2}{\pi} \sum_{n=1}^{\infty} \left [ \frac{1}{2n - 1} \sin (2n-1)x \right] \\ &= \frac{1}{2} - \frac{2}{\pi} \left ( \sin x + \frac{1}{3} \sin 3x + \frac{1}{5} \sin 5x + \cdots \right ) \end{align} \end{split}\]

以上より，与えられた関数 \(f(t)\) のフーリエ級数展開を求めることができた．

補足
3行目から4行目の変換は \(k\) が偶数のときは項が0となるので奇数のみを扱うよう \(k=2n-1\) として式を整理している．

Pythonによるフーリエ級数展開の実装

では，本日説明したフーリエ級数展開をPythonで実装する．まずは時刻 \(t\) の関数 \(f(t)\) を定義する．

from sympy import symbols, cos, sin, pi
x = symbols('x')

f = 1 + 0.25 * cos(x) -1.1 * sin(2*x) + cos(3*x) - 0.4 * sin(4*x)
f

\[\displaystyle - 1.1 \sin{\left(2 x \right)} - 0.4 \sin{\left(4 x \right)} + 0.25 \cos{\left(x \right)} + \cos{\left(3 x \right)} + 1\]

from sympy.plotting import plot
plot(f, xlim=(-pi, pi) , ylim=(-5, 5))

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

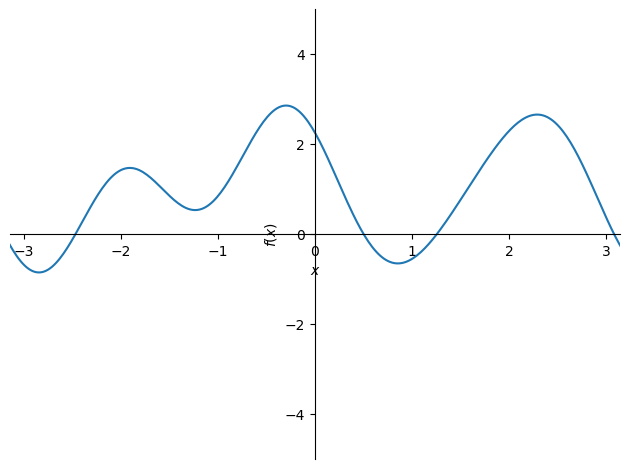
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x111682370>

導出したフーリエ係数 \(a_0, a_k, b_k\) を実装する．

from sympy import Integral
k = symbols('k')
a_0 = Integral(f, (x, -pi, pi)) / (2 * pi)
a_0

\[\displaystyle \frac{\int\limits_{- \pi}^{\pi} \left(- 1.1 \sin{\left(2 x \right)} - 0.4 \sin{\left(4 x \right)} + 0.25 \cos{\left(x \right)} + \cos{\left(3 x \right)} + 1\right)\, dx}{2 \pi}\]

a_k = Integral(f * cos(k * x), (x, -pi, pi)) / pi
a_k

\[\displaystyle \frac{\int\limits_{- \pi}^{\pi} \left(- 1.1 \sin{\left(2 x \right)} - 0.4 \sin{\left(4 x \right)} + 0.25 \cos{\left(x \right)} + \cos{\left(3 x \right)} + 1\right) \cos{\left(k x \right)}\, dx}{\pi}\]

b_k = Integral(f * sin(k * x), (x, -pi, pi)) / pi
b_k

\[\displaystyle \frac{\int\limits_{- \pi}^{\pi} \left(- 1.1 \sin{\left(2 x \right)} - 0.4 \sin{\left(4 x \right)} + 0.25 \cos{\left(x \right)} + \cos{\left(3 x \right)} + 1\right) \sin{\left(k x \right)}\, dx}{\pi}\]

定義できたので，フーリエ係数の計算を実行する．今回は\(k=3\)まで展開してみよう．具体的には\(k\)番目の項を変数として定義していたのでsubs()で代入し，上記で定義した\(a_k,b_k\)の積分を.doit()で実行できる．

a_0.doit()

\[\displaystyle 1\]

a_1 = a_k.subs(k, 1).doit()
a_1

\[\displaystyle 0.25\]

a_2 = a_k.subs(k, 2).doit()
a_2

\[\displaystyle 0\]

a_3 = a_k.subs(k, 3).doit()
a_3

\[\displaystyle 1.0\]

b_0 = b_k.subs(k, 0).doit()
b_0

\[\displaystyle 0\]

b_1 = b_k.subs(k, 1).doit()
b_1

\[\displaystyle 0\]

b_2 = b_k.subs(k, 2).doit()
b_2

\[\displaystyle -1.1\]

b_3 = b_k.subs(k, 3).doit()
b_3

\[\displaystyle 0\]

計算された \(k=3\) までのフーリエ係数をもとにフーリエ級数展開する．

ff_approx = a_0.doit() + a_1 * cos(x) + b_1 * sin(x) + a_2 * cos(2*x) + b_2 * sin(2*x) + a_3 * cos(3*x) + b_3 * sin(3*x)

omega_0は変数Tを含むのでsubs()で代入する．

ff_approx

\[\displaystyle - 1.1 \sin{\left(2 x \right)} + 0.25 \cos{\left(x \right)} + 1.0 \cos{\left(3 x \right)} + 1\]

近似対象と比較をするために同時にプロットしてみる．

plot(f, ff_approx, xlim=(-pi, pi))

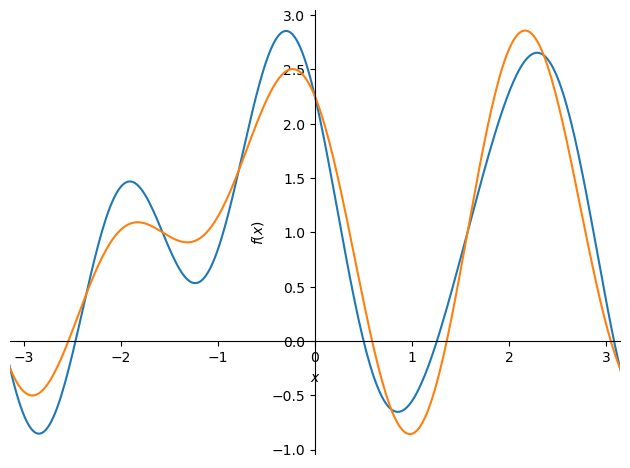
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x12a6ba790>

区間外もプロットしてみる．

plot(f, ff_approx, xlim=(-2*pi, 2*pi))

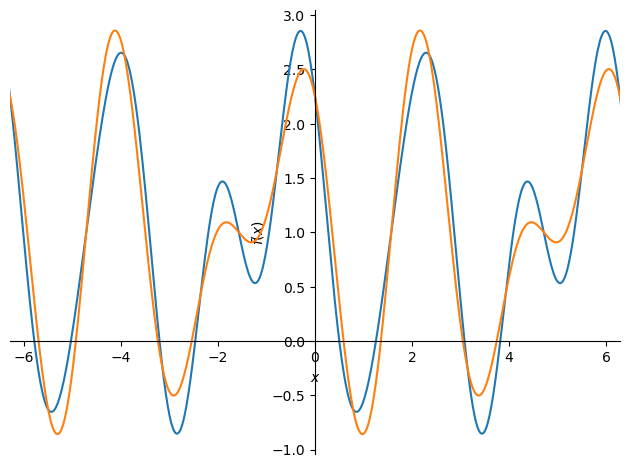
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x12a774730>