フーリエ変換

フーリエ級数の近似区間

フーリエ級数展開・複素フーリエ級数展開では区間上の関数について基本周波数 \(\omega_0 = 2\pi / T\) を整数倍した \(\omega_0, 2\omega_0, 3\omega_0, \ldots\) の周波数を持つ波の足し合わせで表現するため，区間外の領域の関数は近似することができなかった．

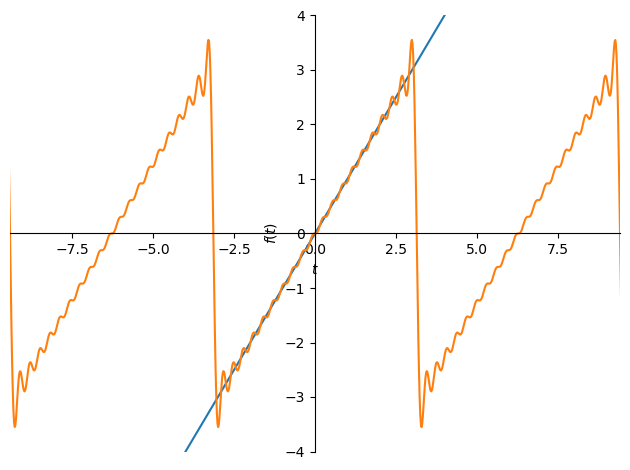
具体例として，\(y=t\) という関数でこの近似区間の問題を可視化してみる．sympyのフーリエ級数展開の関数を用いる．

from sympy import symbols, pi, fourier_series
from sympy.plotting import plot

t = symbols('t')
f = t # f(t) = tの定義

ff = fourier_series(f, (t, -pi, pi)) # フーリエ級数展開を実行
ff_approx = ff.truncate(20) # 第20項目まで計算

plot(f, ff_approx, xlim=(-3*pi, 3*pi), ylim=(-4, 4)) # 区間外まで可視化

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x10f4baa60>

このように区間外では近似された関数が繰り返されているのがわかるかと思う．これはフーリエ級数展開が周期関数である正弦波の重ね合わせで構成されているからである．しかしながら，与えられた関数や信号がこのような周期性を持つ場合は限られており，関数や信号の解析を行う上で 非周期 な対象へのフーリエ解析の方法が求められる．本講義では，非周期関数への拡張を行なった フーリエ変換 を学ぶことが目標である．

フーリエ変換

フーリエ変換 は無限区間で定義されかつ非周期関数に対するフーリエ解析の方法である．これまでのフーリエ級数展開と同様に，フーリエ変換は時間の関数を 周波数 の関数へ変換可能であり，与えられた関数にどのような周波数が含まれているかを解析することができる．一方で，フーリエ変換では周波数の関数から時間の関数へ変換する 逆フーリエ変換 も定義されている．フーリエ変換は

\[ F \left ( \omega \right ) = \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \]

として定義され，

逆フーリエ変換は

\[ f(t) = \frac{1}{2 \pi} \int^{\infty}_{-\infty} F \left ( \omega \right ) e^{i \omega t} d \omega \]

で与えられる．

区分求積法からのフーリエ変換の導出

では，フーリエ変換と逆フーリエ変換を複素フーリエ級数と複素フーリエ係数から導出する．複素フーリエ級数と複素フーリエ係数は以下で定義されていた．

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \\ C_k &= \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \end{align} \end{split}\]

ここから \(T\) を無限に大きくしたときの複素フーリエ級数展開を考える．そのために上記の二式に含まれる基本周波数 \(\omega_0\) について，足し合わされる整数倍の周波数 \(k \omega_0\) を \(\omega_k\) と表記する．

\[ \omega_k = k \omega_0, k = 0, \pm 1, \pm 2, \cdots \]

\(\omega_k\) を使って複素フーリエ級数と係数を整理する．複素フーリエ級数は

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \\ &= \sum_{k=-\infty}^{\infty} C_k e^{i \omega_k t} \\ \end{align} \end{split}\]

となり，複素フーリエ係数は，

\[\begin{split} \begin{align} C_k &= \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \\ &= \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-i \omega_k t} dt \end{align} \end{split}\]

となる．ここで，\(\omega_{k+1}\) と \(\omega_k\) は \(\omega_0\) の整数倍であることから次のような性質を導ける．

\[ \omega_{k+1}-\omega_k=\omega_0=\frac{2\pi}{T} \]

この差を \(\Delta \omega\) として定義する．

\[ \Delta \omega = \omega_{k+1}-\omega_k=\omega_0=\frac{2\pi}{T} \]

ここで，フーリエ係数を以下のように \(F(\omega_k) := \int_{-T/2}^{T/2} f(t) e^{-i \omega_k t} dt\) とすると，

\[ C_k = \frac{F(\omega_k)}{T} = \frac{F(\omega_k)}{2\pi} \Delta \omega \]

となる．そして，\(f(t)\) に \(C_k\) を代入する．

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{i \omega_k t} \\ &=\sum_{k=-\infty}^{\infty} \frac{F\left(\omega_k\right)}{2 \pi} e^{i \omega_k t} \Delta \omega \end{align} \end{split}\]

ここで重要なのは，区分求積法の形式

\[ \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d\omega \approx \sum_{k=-\infty}^{\infty} F(\omega_k) e^{i \omega_k t} \Delta \omega \]

に近いている点である．

そこで，区間 \(T\) を \(\infty\) にするために積分の定義（区分求積法）から複素フーリエ級数を整理する．先ほどの式は

\[ f(t) = \frac{1}{2\pi} \sum_{k=-\infty}^{\infty} F(\omega_k) e^{i \omega_k t} \Delta \omega \]

と整理され，これはまさに，

\[ \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d\omega \]

の積分（リーマン和）となっている．ただし，厳密には，関数 \(f(t)\) が \([-\infty, \infty]\) で 区分的に滑らか で，絶対可積分 であるという条件のもとで，有限区間 \(T\) を無限区間に拡張すると \(T \rightarrow \infty\) のとき \(\Delta \omega\) は \(2\pi / T\) より \(\Delta \omega = 0\) に収束することが必要となる（無限大の範囲で積分したときに積分結果が発散してしまわないようにするため）．

区分求積法

\[ \int_{a}^{b} f \left ( x \right ) dx = \displaystyle \lim_{N \to \infty} \sum_{k=0}^{N-1} f \left ( x_k \right ) \Delta x \]

厳密には無限区間 \([-\infty, \infty]\) での積分より，広義積分として扱う必要があるが後述する絶対可積分の条件よりこのように考えて良い．

このとき，\(F(\omega)\) の周期 \(T\) を無限大にした形である，時刻 \(t\) の関数 \(f(t)\) から周波数 \(\omega\) の関数 \(F(\omega)\)への変換を フーリエ変換 と呼び，以下で与えられる．

\[ F \left ( \omega \right ) = \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \]

フーリエ変換は式の通り，\(-\infty\) から \(\infty\) までのすべての時刻 \(t\) にわたる積分で周波数の関数へ変換できる． 一方で，周波数 \(\omega\) の関数 \(F(\omega)\) から時刻 \(t\) の関数 \(f(t)\) への変換を 逆フーリエ変換 と呼び，以下で与えられる．

\[ f(t) = \frac{1}{2 \pi} \int^{\infty}_{-\infty} F \left ( \omega \right ) e^{i \omega t} d \omega \]

式の通り，\(-\infty\) から \(\infty\) までのすべての周波数 \(\omega\) を持つ関数の重ね合わせと解釈できる．

フーリエ変換の条件

フーリエ変換の導出で登場したフーリエ変換を行うための条件について紹介する． 前述のの変形を行うには，関数 \(f(t)\) が区間 \([-\infty, \infty]\) で区分的に滑らかで，絶対可積分である必要があった．

ここで関数 \(f(t)\) が区間 \([-\infty, \infty]\) で区分的に滑らかであるとは，

• 関数 \(f(t)\) と導関数 \(f'(t)\) が連続（滑らかな関数）

• 1周期の間に有限個の不連続点しかもたず，かつ，どの不連続点 \(t_0\)に対しても \(f(t_0-0)\) と \(f(t_0+0)\) が有限の値として存在する関数（区分的に連続な関数）

という二条件を満たした 「関数 \(f(t)\) と導関数 \(f'(t)\) がともに区分的に連続な関数である」ということを示す．

そして，絶対可積分であるとは，絶対値をとって積分したときに発散しないということを示す．

\[ \int_{-\infty}^{\infty}|f(x)| dx<\infty \]

直交性からのフーリエ変換の導出

では，フーリエ変換と逆フーリエ変換を複素フーリエ級数と複素フーリエ係数の直交性から導出する．複素フーリエ級数と複素フーリエ係数は以下で定義されていた．

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \\ C_k &= \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \end{align} \end{split}\]

この複素フーリエ級数の関数系は \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) であった．ここで，より連続的な周波数をもつ \(\omega\) に関する関数系 \(\{e^{i\omega t}|\omega\in\mathbb{R}\}\) を考える．この関数系の要素 \(e^{i\omega_1 t}\) と \(e^{i\omega_2 t}\) について，内積

\[ \int_{-\infty}^{\infty}\ f(x) \overline{g(x)} dx= 0 \]

が成り立つことを確認する．具体的に，

\[\begin{split} \begin{align} \int_{-\infty}^{\infty} e^{i\omega_1 t} \overline{e^{i\omega_2 t}} dt &= \int_{-\infty}^{\infty} e^{i\omega_1 t} e^{-i\omega_2 t} dt \\ &= \int_{-\infty}^{\infty} e^{i (\omega_1-\omega_2) t} dt \\ &= 2 \pi \delta (\omega_1-\omega_2) \end{align} \end{split}\]

ここで \(\delta\) は ディラックのデルタ関数 とよばれる超関数である．

デルタ関数

デルタ関数は任意の連続関数 \(f(x)\) に対して

\[ \int_{-\infty}^{\infty} f(x) \delta(x) dx = f(0) \]

を満たす関数のことをいう．ここで \(\delta(x)=0, x\neq 0\) であり，デルタ関数自身を積分すると

\[ \int_{-\infty}^{\infty} \delta(x) dx = 1 \]

となる．このほか，デルタ関数には平行移動に関する性質

\[ \delta(x - a) = 0, (x \neq a) \]

\[ \int_{-\infty}^{\infty} f(x) \delta(x - a) dx = f(a) \]

や，フーリエ変換に関する性質

\[ \delta(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{i\omega x} d\omega \]

を持つ．

これを利用して上記の内積の式が得られている．さらに，\(\omega_1 -\omega_2 \neq 0\) ならば，

\[ \begin{align} \int_{-\infty}^{\infty} e^{i\omega_1 t} \overline{e^{i\omega_2 t}} dt = 2 \pi \delta (\omega_1-\omega_2) = 0 \end{align} \]

であり，直交関数系であることもわかる．これより，\(k\omega\) という整数倍の周波数を連続値 \(\omega\) で基底を作れたことになる．

これにしたがって，複素フーリエ級数

\[ \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \end{align} \]

は \(k \omega\) が連続値になったことより，総和を積分に修正する必要がある．つまり，

\[ f(t) = \int_{-\infty}^{\infty} G(\omega) e^{i\omega t} d\omega \]

である．これまでの直交性からの導出と同じように両辺に \(e^{-i\omega t}\) をかける．ただし，積分の \(\omega\) とこのかける \(\omega\) は別の変数であるので次のように変数名を変えておく．

\[ f(t)e^{-i\omega t} = \left\{\int_{-\infty}^{\infty} G(s) e^{is t} ds\right\} e^{-i\omega t} \]

次に，両辺を積分する．

\[\begin{split} \begin{align} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt &= \int_{-\infty}^{\infty}\left\{\int_{-\infty}^{\infty} G(s) e^{is t} ds\right\} e^{-i\omega t}dt \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} G(s) e^{is t} e^{-i\omega t} dt ds\\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} G(s) e^{i (s - \omega) t} dt ds\\ &= \int_{-\infty}^{\infty} G(s) \left\{\int_{-\infty}^{\infty} e^{i (s - \omega) t} dt \right\} ds \\ &= \int_{-\infty}^{\infty} G(s) \delta (s - \omega) ds \\ &= 2 \pi G(\omega) \end{align} \end{split}\]

よって，

\[ G(\omega) = \frac{1}{2\pi} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \]

ここで，

\[ F(\omega) = 2 \pi G(\omega) \]

とすると，

\[ F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \]

が得られ，これが関数 \(f(t)\) の フーリエ変換 となる．また，

\[\begin{split} \begin{align} f(t) &= \int_{-\infty}^{\infty} G(\omega) e^{i\omega t} d\omega \\ &= \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) e^{i\omega t} d\omega \end{align} \end{split}\]

が得られ，これは 逆フーリエ変換 といわれる．

二重積分の順序を入れ替えるときの注意

上記の導出では，次のように二重積分の順序を入れ替えている：

\[ \int_{-\infty}^{\infty} \left\{ \int_{-\infty}^{\infty} G(s) e^{i s t} ds \right\} e^{-i\omega t} dt = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} G(s) e^{i (s - \omega) t} dt ds \]

このように積分の順序を入れ替えるためには，関数の 絶対可積分性 が必要となる．

\[ \iint_{\mathbb{R}^2} \left| G(s) e^{i(s - \omega)t} \right| dt ds < \infty \]

が満たされていれば，積分の順序を入れ替えても良い．これは区分求積法と同等の条件である．

波の重ね合わせ

フーリエ級数展開，複素フーリエ級数展開，フーリエ変換はすべて時刻 \(t\) に関する関数 \(f(t)\) を異なる周波数 \(\omega\) の波の重ね合わせで表現することを試みている．複素フーリエ級数とフーリエ変換を見比べてみると

複素フーリエ級数展開

\[ f(t) = \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} , \quad C_k = \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \]

フーリエ変換・逆フーリエ変換

\[ f(t) = \frac{1}{2 \pi} \int^{\infty}_{-\infty} F \left ( \omega \right ) e^{i \omega t} d \omega, \quad F \left ( \omega \right ) = \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \]

となり，これらのフーリエ解析方法は変換後の周波数の扱いが整数倍であるか？それとも連続的に定義されているか？の違いで区別される．そして，周波数 \(\omega\) に関する情報はフーリエ級数の場合は 離散スペクトル ，フーリエ変換の場合は 連続スペクトル と呼ばれる

具体例

では，以下の関数をフーリエ変換しよう．

\[\begin{split} f(t) = \begin{cases} e^{-t} & 0 \leq t \\ 0 & t < 0 \end{cases} \end{split}\]

解答はクリックで確認できる．

フーリエ変換の式 \(F(\omega)\) の式に当てはめて計算する．

\[\begin{split} \begin{align} F \left ( \omega \right ) &= \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \\ &= \int^{0}_{-\infty} 0 \cdot e^{-i\omega t} dt + \int^{\infty}_{0} e^{-t} e^{-i\omega t} dt \\ &= \int^{\infty}_{0} e^{-\left ( 1 + i\omega \right )t} dt \\ &= \left [ \frac{-1}{1+i\omega} e^{ -\left ( 1 + i\omega \right )t} \right ]^{\infty}_{0} \\ &= \frac{- e^{- \left ( 1 + i\omega \right ) \cdot \infty}}{1+i\omega} - \frac{- e^{- \left ( 1 + i\omega \right ) \cdot 0}}{1+i\omega} \\ &= \frac{1}{1 + i\omega} \\ &= \frac{1-i\omega}{1 + \omega^2} \end{align} \end{split}\]

ここで \(e^{-\infty}e^{ - i\omega \infty} = e^{-\infty}e^{ i\omega \infty} = 0\) を利用してる．以上より，\(f(t)\) のフーリエ変換 \(F(\omega)\) を計算することができた．

Pythonでフーリエ変換

では，Pythonでフーリエ変換を実行する．まず注意点として，フーリエ変換は無限区間で周期を持たない非周期関数 \(f(t)\) を時間の関数から周波数の関数へ変換できるが，そのための条件は \(f(t)\) が区間 \([-\infty,\infty]\) 区分的に滑らかで絶対可積分である必要があった．絶対可積分とは，絶対値をとって積分したときに発散しないことを示している．この条件は厳しく，例えば \(f(\pm \infty)=0\)とならない場合は，絶対可積分とならない．また広義積分をするので，解析的に求められない場合もある．そのため，\(f\) の定義によってはエラーとなるので注意されたい．

以下でフーリエ変換する関数を定義する

from sympy import symbols, exp
from sympy.plotting import plot

t = symbols('t', real=True)
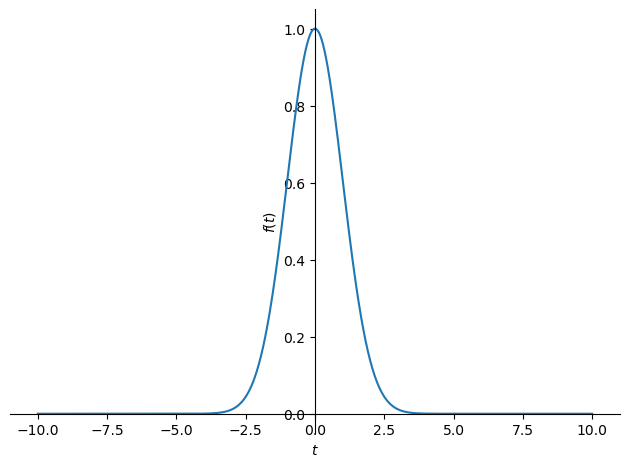
f = exp(-t**2/2)
f

\[\displaystyle e^{- \frac{t^{2}}{2}}\]

plot(f)

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x10d7f9430>

Sympyでは，時刻の変数 \(t\) と周波数の変数 \(\omega\) を定義して，fourier_transform(関数，t, omega)でフーリエ変換できる．ただし，解析的に求められない場合は，式の代わりに，FourierTransformクラスが帰ってくる．

from sympy import fourier_transform
omega = symbols('omega', real=True)
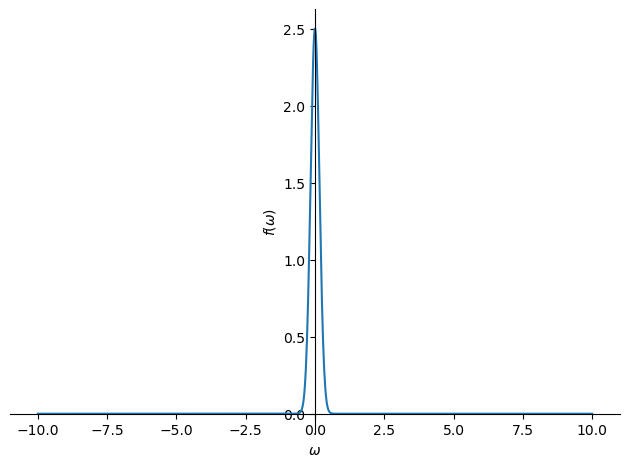
ft = fourier_transform(f, t, omega)
ft

\[\displaystyle \sqrt{2} \sqrt{\pi} e^{- 2 \pi^{2} \omega^{2}}\]

時刻から周波数の関数に変換されていることを確認するためにフーリエ変換後のグラフをプロットする

plot(ft)

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x1268e7b20>

Sympyでは，フーリエ変換と同様に，時刻の変数 \(t\) と周波数の変数 \(\omega\) を定義して，inverse_fourier_transform(関数, omega, t)で逆フーリエ変換できる．ただし，解析的に求められない場合は，式の代わりに，InverseFourierTransformクラスが帰ってくる．

from sympy import inverse_fourier_transform
ift = inverse_fourier_transform(ft, omega, t)
ift

\[\displaystyle e^{- \frac{t^{2}}{2}}\]

同様に周波数から時刻の関数に変換されていることを確認するために逆フーリエ変換後のグラフをプロットする．

plot(ift)

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x126b1b700>

フーリエ変換の性質

フーリエ変換には微分方程式の適用や周波数解析において役立つ性質がいくつかある．

フーリエ変換の線形性

関数 \(f(t)\) から周波数に関する関数 \(F(\omega)\) を得るフーリエ変換を \(\mathcal{F}(f(t))\) とする．

\[ F \left ( \omega \right ) = \mathcal{F}(f(t)) = \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \]

このときフーリエ変換には以下の線形性の性質がある．

\(f(t)\) の定数倍 \(cf(t)\) のフーリエ変換の性質

\[ \mathcal{F}(cf(t)) = c \mathcal{F}(f(t)) \]

証明はクリックで確認できる．

\[\begin{split} \begin{align} \mathcal{F}(cf(t)) &= \int^{\infty}_{-\infty} c f\left ( t \right ) e^{-i\omega t} dt \\ &= c \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \\ &= c \mathcal{F}(f(t))\\ \end{align} \end{split}\]

\(f(t)\) と　\(g(t)\) の和に関するフーリエ変換の性質

\[ \mathcal{F}(f(t) \pm g(t)) = \mathcal{F}(f(t)) \pm \mathcal{F}(g(t)) \]

証明はクリックで確認できる．

\[\begin{split} \begin{align} \mathcal{F}(f(t) \pm g(t)) &= \int^{\infty}_{-\infty} \left \{ f\left ( t \right ) \pm g\left ( t \right ) \right \} e^{-i\omega t} dt \\ &= \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t} dt \pm \int^{\infty}_{-\infty} g\left ( t \right ) e^{-i\omega t} dt \\ &= \mathcal{F}(f(t)) \pm \mathcal{F}(g(t)) \end{align} \end{split}\]

フーリエ変換の導関数の性質

関数 \(f(t)\) のフーリエ変換 \(\mathcal{F}(f(t))\) と関数 \(f(t)\) の\(n\) 次導関数 \(f^{(n)}(t)\) には以下の関係がある．

\[ \mathcal{F}(f^{(n)}(t)) = (i \omega)^n \mathcal{F}(f(t)) \]

これは導関数 \(f^{(n)}(t)\) のフーリエ変換の結果 \(\mathcal{F}(f^{(n)}(t))\) は元の関数 \(f(t)\) のフーリエ変換後の周波数領域で \(i \omega\) をかけることに等しい．

証明はクリックで確認できる．

\[\begin{split} \begin{align} \mathcal{F}(f'(t)) &= \int^{\infty}_{-\infty} f' \left ( t \right ) e^{-i\omega t} dt\\ &= \left [ f \left ( t \right ) e^{-i \omega t} \right ]^{\infty}_{-\infty} - \int^{\infty}_{-\infty} f \left ( t \right ) \left ( - i \omega \right) e^{-i\omega t} dt\\ &= i \omega \int^{\infty}_{-\infty} f \left ( t \right ) e^{-i\omega t} dt\\ &= i \omega \mathcal{F}(f(t)) \end{align} \end{split}\]

第二行目では絶対可積分の条件 \(f(\pm \infty)=0\) を利用している．これを \(f'(t), f''(t),\ldots\) と計算すると導関数の性質を導出できる．

フーリエ変換の時刻と周波数のシフト則

フーリエ変換の時刻のシフト則

関数 \(f(t)\) を \(t_0\) だけ平行移動した関数 \(f(t-t_0)\) のフーリエ変換は次の性質がある．

\[ \mathcal{F}(f(t-t_0)) = e^{-i \omega t_0} \mathcal{F}(f(t)) \]

証明はクリックで確認できる．

\[\begin{split} \begin{align} \mathcal{F}(f(t-t_0)) &= \int^{\infty}_{-\infty} f\left ( t - t_0 \right ) e^{-i\omega t} dt \\ &= \int^{\infty}_{-\infty} f\left ( s \right ) e^{-i\omega \left ( s + t_0 \right)} ds \\ &= \int^{\infty}_{-\infty} f\left ( s \right ) e^{-i\omega s} e^{-i\omega t_0 } ds \\ &= e^{-i\omega t_0 } \int^{\infty}_{-\infty} f\left ( s \right ) e^{-i\omega s } ds \\ &= e^{-i\omega t_0 } \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i\omega t } dt \\ &= e^{-i \omega t_0} \mathcal{F}(f(t)) \end{align} \end{split}\]

フーリエ変換の周波数のシフト則

関数 \(f(t)\) のフーリエ変換後の \(F(\omega)\) を \(\omega_0\) だけ平行移動した関数 \(F(\omega-\omega_0)\) には以下の性質がある．

\[ \mathcal{F}(f(t) e^{i \omega_0 t}) = F(\omega - \omega_0) \]

証明はクリックで確認できる．

\[\begin{split} \begin{align} \mathcal{F}(f(t) e^{i \omega_0 t}) &= \int^{\infty}_{-\infty} f\left ( t \right ) e^{i \omega_0 t } e^{-i\omega t } dt \\ &= \int^{\infty}_{-\infty} f\left ( t \right ) e^{-i \left ( \omega - \omega_0 \right ) t } dt \\ &= F(\omega - \omega_0) \end{align} \end{split}\]