周期関数

周期関数#

\(\sin\)関数と\(\cos\)関数は 正弦波 とも呼ばれ，この正弦波は同じ波が一定間隔で繰り返される 周期関数 である．このとき波が繰り返される一定間隔のことを 周期 と呼ぶ．周期を正の定数 \(T\) として，周期関数 \(f\) は

\[ f(x+T) = f(x) \]

という性質を持つ．\(\sin\)関数と\(\cos\)関数もまた周期 \(T=2\pi\) の周期関数であり，三角関数の性質から，

\[ \sin(x+2\pi) = \sin(x), \quad \cos(x+2\pi) = \cos(x) \]

となるのは自明である．\(\sin\)関数と\(\cos\)関数の周期 \(T=2\pi\) のようにこの周期関数の性質を満たす最小の正の定数のことを 基本周期 と言う．\(2T, 3T, ...\)も周期関数の性質を満たすので周期と言えるが，これらの違いについて注意されたい．

Pythonによる実装#

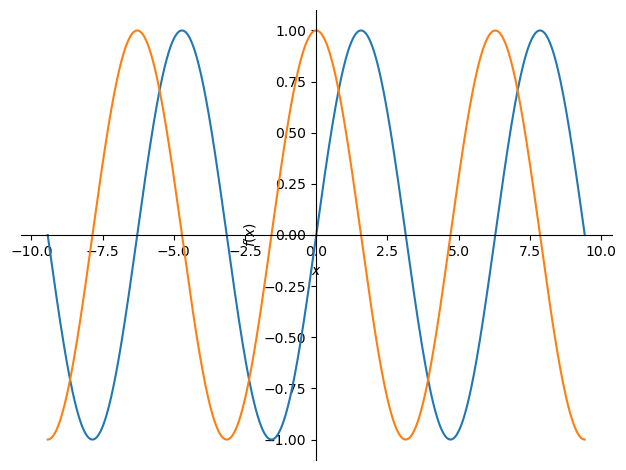
では，\(\sin\)関数と\(\cos\)関数の周期関数としての性質をsympyで確認し，プロットしてみよう．

from sympy import symbols, sin, cos, pi
from sympy.plotting import plot

x = symbols('x')
T = symbols('T')

f_sin = sin(x + T)
f_cos = cos(x + T)
plot(f_sin.subs(T, 2*pi), f_cos.subs(T, 2*pi), (x, -3*pi, 3*pi))

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
../../_images/dc0bf32fa8e131ca1da868a608574179560d219b79e790e69b0bf457da8317e2.png 
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x10f6ab400>
Contents