直接積分形

次の一階常微分方程式と呼ばれる微分方程式をこれまでの微積分の知識を使って解くことを試みる．関数 \(f(x,y)\) が変数\(x\)にのみ依存した関数\(g(x)\)であるときの場合を考える．すなわち，

\[ \begin{align} \frac{dy}{dx} = g(x) \end{align} \]

の関数の形式の微分方程式である．前述の例は \(g(x)=x\) のときの直接積分形による解法である．

直接積分形の解法

与えられた一階常微分方程式が上記のような形状に変形可能であるとき，次のステップを踏むことで未知関数 \(y=y(x)\) を計算できる．

まず，微分方程式の両辺に\(dx\)をかけると以下のようになる

\[ \begin{align} dy = g(x)dx \end{align} \]

式を見てわかるように，\(x\)と\(y\)の項がそれぞれ両辺に移項できたことがわかる．続いて両辺を積分する．

\[ \begin{align} \int dy = \int g(x)dx \end{align} \]

この積分を求めるとで以下の微分方程式の解である未知関数 \(y(x)\)が得られる．

\[ \begin{align} y(x) = \int g(x) dx + C \end{align} \]

ただし，\(C\)は積分定数である．これは後述する変数分離法で\(y\)に関する項がないときの特殊な形式である．

直接積分形の具体例

では，次の微分方程式の直接積分形で解いてみよう．以下の微分方程式は \(g(x)=x^2+1\) のときの場合である．

\[ \begin{align} \frac{dy}{dx} = x^2 + 1 \end{align} \]

解答はクリックで確認できる．

まず，両辺に \(dx\) をかけると以下のようになる．

\[ \begin{align} dy = \left(x^2 + 1\right) dx \end{align} \]

続いて，両辺を積分することを考える．

\[ \begin{align} \int 1 dy = \int \left(x^2 + 1\right) dx \end{align} \]

積分すると以下の微分方程式の解が得られる．

\[ \begin{align} y = \frac{x^3}{3} + x + C \end{align} \]

ただし，\(C\)は積分定数である．実際に結果を微分した結果も確認されたい．与えられた微分方程式になるはずである．

Pythonによる実装

上記の微分方程式をsympyで実装する．前述した式変形はあくまでも手計算での方法であり，sympyを利用すると（シンボリックに計算できる微分方程式の形式であれば）式変形なしに解を求めることができる．

from sympy import symbols, Eq, Derivative, Function, dsolve

# 変数と未知関数の定義
x = symbols('x')
y = Function('y')(x)

# dy/dxの定義
dy = Derivative(y, x)

# 微分方程式の定義
eq = Eq(dy, x**2+1)

# 微分方程式を解く
y_ = dsolve(eq, y)
y_

\[\displaystyle y{\left(x \right)} = C_{1} + \frac{x^{3}}{3} + x\]

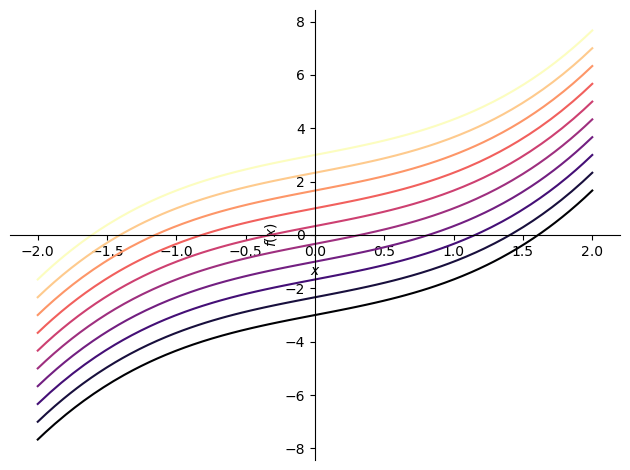
一般解もプロットしてみる．前述した愚直に \(C\) を代入する方法ではなくここではリストを使ってプロットする方法を紹介する．

import numpy as np
from sympy import plotting
import matplotlib.pyplot as plt

N = 10

eqs = []
for c in np.linspace(-3, 3, N):
    eqs.append(y_.rhs.subs(symbols('C1'), c))
p = plotting.plot(*eqs, (x, -2, 2), show=False)

cm = plt.get_cmap('magma', N)
for i in range(cm.N):
    p[i].line_color = cm(i)
p.show()