一階線形同次微分方程式

線形微分方程式

線形微分方程式とは線形性を持つ微分方程式である．微分方程式を

\[ F(x,y,y')=0 \]

と定義する，ここで\(y'=\frac{dy}{dx}\)であり，実定数 \(\alpha,\beta\)に対して，

\[ \begin{align} F\left(x, \alpha y_1+\beta y_2, \alpha y_1'+\beta y_2'\right)= \alpha F \left(x, y_1, y_1'\right)+\beta F\left(x, y_2, y_2'\right) \end{align} \]

が成立すれば微分方程式が線形であり，その微分方程式を線形微分方程式と呼ぶ．

一階線形微分方程式

ここでは一階線形微分方程式に着目し，その解法を紹介する．まず一階線形微分方程式は以下の形式で表される微分方程式である．

\[ \begin{align} \frac{dy}{dx}+p(x)y=q(x) \end{align} \]

ここで\(p(x)\)と\(q(x)\)は\(x\)の関数である．ここで\(p(x)\)と\(q(x)\)はすべての入力に対して0を出力しないという点に留意されたい．もし0を出力する場合，この関数は恒等的に0ではない関数と呼ばれ，この形式の微分方程式は変数分離形に容易に求めることができる．

一階線形同次微分方程式

上記では，\(p(x)\)と\(q(x)\)は恒等的に0ではない関数であると説明したが，ここでは，\(q(x)=0\)のときの微分方程式を考える．このとき微分方程式は以下のように変形できる．

\[ \begin{align} \frac{dy}{dx}+p(x)y=0 \Rightarrow \frac{dy}{dx}=-p(x)y \end{align} \]

このときの微分方程式を一階線形同次微分方程式と呼ぶ．

一階線形同次微分方程式の解法

上記に示した一階線形微分方程式の一般解は変数分離形で容易に計算できる．まず左辺には\(y\)に関する項を，右辺には\(x\)に関する項となるように式変形を行う．

\[\begin{split} \begin{align} \frac{1}{y} \frac{dy}{dx} &= -p(x) \\ \frac{1}{y} dy &= -p(x) dx \end{align} \end{split}\]

次に，両辺を積分する．

\[ \begin{align} \int \frac{1}{y} dy = - \int p(x) dx \end{align} \]

これを解くと，以下の解が得られる．

\[ \begin{align} \ln |y| = - \int p(x) dx + C' \end{align} \]

ここで，\(C'\)は積分定数である．第4回の式展開でも紹介したように，\(\log |y| = x \rightarrow e^x = |y|\) であり，絶対値を外すと，\(y=\pm e^x\) となる．従って，上記の一般解は \(y(x)\)の形に書き換えることができる．

\[\begin{split} \begin{align} y(x) &= \pm e^{-\int p(x) \, dx + C'} \\ &= \pm e^{C'} e^{-\int p(x) \, dx} \\ &= C e^{-\int p(x) \, dx} \end{align} \end{split}\]

ここで，\(C=\pm e^{C'}\)とした．

一階線形同次微分方程式の具体例

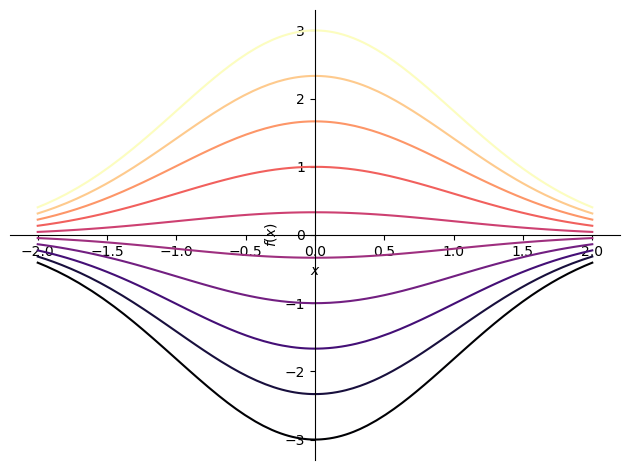
では，次の一階線形同次微分方程式を解いてみよう．以下の微分方程式は \(p(x)=x\) のときの場合である．

\[ \begin{align} \frac{dy}{dx}+xy=0 \end{align} \]

解答はクリックで確認できる．

まず，左辺に \(y\) のみ，右辺に \(x\) の項のみとなるよう変数分離形に整理すると，

\[\begin{split} \begin{align} \frac{dy}{dx} &= -xy \\ \frac{1}{y} dy &= -x dx \end{align} \end{split}\]

となる．続いて，両辺を積分する．

\[ \begin{align} \int \frac{1}{y} dy = - \int x dx \end{align} \]

積分定数を \(C'\) とすると以下となる．

\[ \begin{align} \ln |y| = - \frac{x^2}{2} + C' \end{align} \]

\(y\) について整理すると，

\[\begin{split} \begin{align} y &= \pm e^{- \frac{x^2}{2} + C'} \\ &= \pm e^{C'} e^{- \frac{x^2}{2}} \\ &= C e^{- \frac{x^2}{2}} \end{align} \end{split}\]

となり，一般解が得られた．ここで，\(C=\pm e^{C'}\)とした．

Pythonによる実装

では，上記の微分方程式をsympyで解く．単一のセルで作成したが，各行での動作は前回の講義のようにStep-by-stepで確認されたい．

from sympy import symbols, Eq, Derivative, Function, dsolve

# 変数と未知関数の定義
x = symbols('x')
y = Function('y')(x)

# dy/dxの定義
dy = Derivative(y, x)

# 微分方程式の定義
eq = Eq(dy + x*y, 0)

# 微分方程式を解く
y_ = dsolve(eq, y)
y_

\[\displaystyle y{\left(x \right)} = C_{1} e^{- \frac{x^{2}}{2}}\]

import numpy as np
from sympy import plotting
import matplotlib.pyplot as plt

N = 10

eqs = []
for c in np.linspace(-3, 3, N):
    eqs.append(y_.rhs.subs(symbols('C1'), c))
p = plotting.plot(*eqs, (x, -2, 2), show=False)

cm = plt.get_cmap('magma', N)
for i in range(cm.N):
    p[i].line_color = cm(i)
p.show()