ニュートン・ラプソン法

ニュートン法（Newton’s method） または ニュートン・ラプソン法（Newton-Raphson method） は方程式の解を数値計算から近似的に求めるための方法である．アイデアは初期の推定値からスタートし，関数の値とその導関数を使用して新しい推定値の更新を反復的に計算することで，近似解を得るものである．

定義域 \(x \in \mathbb{R}\) で定義される関数 \(f: \mathbb{R} \rightarrow \mathbb{R}\) について

\[ f(x) = 0 \]

となる \(x\) を求める．そのために，\(x\) について初期値 \(x_0\) を適当に取り，以下の反復式に従って \(x\) を更新する．

\[ x_{n+1} = x_{n} - \frac{f(x_n)}{f'(x_n)} \]

このとき，\(n\) は現在の反復数，\(x_n\) は現在の\(x\)の推定値，\(f(x_n)\) はそのときの関数の値，\(f'(x_n)\) はその導関数である．この反復式は接線の方程式

\[ y = f'(x_n)(x - x_n) + f(x_n) \]

を考えると今考えているのは，\(f(x)=0\) となる \(x\) であり，この接線が \(x\)軸 交わる点 \((x_{n+1},0)\) は以下のように求められる．

\[\begin{split} \begin{align} 0 &= f'(x_n)(x_{n+1} - x_n) + f(x_n) \\ f'(x_n)x_{n+1} &= f'(x_n)x_n - f(x_n) \\ x_{n+1} &= x_n - \frac{f(x_n)}{f'(x_n)} \end{align} \end{split}\]

つまり，この反復式は接線を使って \(f(x)=0\) を解いていることに他ならない．これを反復することで真の解に近い近似値を得ることができる．

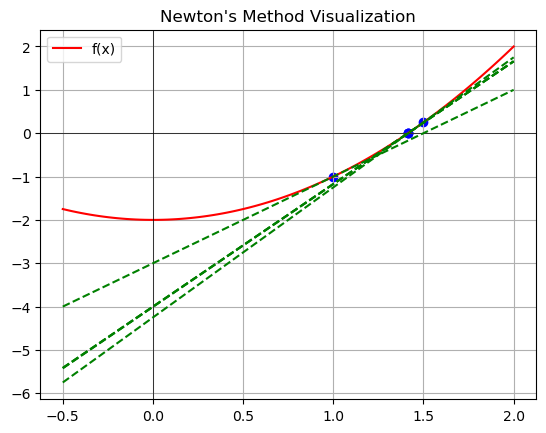
これをPythonで実装する．今回は \(f(x) = x^2 - 2\) について \(f(x)=0\) となる \(x\) をニュートン法によって求める．計算すると，\(x=\pm\sqrt{2}\) となる．この解に近い近似解が得られることを次のプログラムで確認する．

import numpy as np
import matplotlib.pyplot as plt

f = lambda x: x**2 - 2
df = lambda x: 2*x

# newtown method
epsilon = 1e-10
x, x0 = 1, 1
x_s = [x0]

for i in range(10):
    x_ = x - f(x) / df(x)
    x_s.append(x_)
    if abs(x_ - x) < epsilon:
        break
    x = x_
    print(i, x)

# plot optimization
x = np.linspace(-0.5, 2.0, 100)

fig, ax = plt.subplots()
ax.plot(x, f(x), 'r-', label='f(x)')
ax.axhline(0, color='black', linewidth=0.5)
ax.axvline(0, color='black', linewidth=0.5)

for i, x_n in enumerate(x_s[:-1]):
    tangent = df(x_n) * (x - x_n) + f(x_n)
    ax.plot(x, tangent, 'g--')

    ax.scatter([x_n], [f(x_n)], color='blue')

ax.set_title("Newton's Method Visualization")
ax.legend()
ax.grid(True)

0 1.5
1 1.4166666666666667
2 1.4142156862745099
3 1.4142135623746899