数理解析の導入

数理解析

数理解析 は自然科学に現れる現象を数理的に解明するための学問である．そのために，極限や微積分といった解析学に基づき，観測された時間や空間で変化する現象を数理的に記述し，その内在するダイナミクスや特性を解析することが数理解析の目的である．

本講義ではまず数理解析の方法として 微分方程式 に焦点を当てる．微分方程式は様々な現象を表現しモデル化する有力な手段であり，その解を求めることで現象の根底に潜むダイナミクスや特性を明らかにすることができる．微分方程式は関数を解とする方程式であり，その適用範囲は多岐に渡るが，解析的に解くことが可能な微分方程式の形式は限定的で，微分・積分を含む微分方程式の解を求めるのは一般的に難易度が高い．

そこで，次に本講義で取り上げるのが フーリエ解析 である．フーリエ解析，特にフーリエ変換やラプラス変換という手法を利用すると、難解な微分方程式も周波数空間で簡単に解くことが可能となる．またフーリエ解析は関数や信号を単純な波の組み合わせで表現することができ，信号処理においても重要な分野である．

このように微分方程式とフーリエ解析ともに，実数・複素数，極限，連続性，微積分といった解析学の知識を基礎として，数理解析学を構成している．本講義の目的は，受講者が数理解析の主要な概念と手法を理解し、具体的には微積分の基礎から始まり、微分方程式とフーリエ解析について深い理解を得ることを期待する．

微分方程式

微分方程式 とは関数の微分（導関数）を含む方程式である．微分が関数の変化を表すと学んだように，このような微分が含まれる微分方程式はある関数の変化の法則を表す式と言える．

具体例を考える．質量が \(m\) の物体を力 \(F\) で動かしたとき，時刻 \(t\) での物体の位置 \(x=x(t)\) は以下の式で与えられる．

\[ m\frac{d^2x}{dt^2}=F \]

これはニュートンの運動方程式（第二法則）と呼ばれる微分方程式であり，同じ力 \(F\) で異なる質量の物体を動かしたとき，質量が大きい物体の方が動くのが遅い（=加速度が小さい）という現象の性質を記述している．では，物体の位置 \(x(t)\) はどのような関数であろうか？第一回では解を紹介するのみとするが今後の講義からその解き方を学ばれたい．

時刻 \(t=0\) のときの位置について \(x(0)=0\) として，また力 \(F\) が一定であるという前提のもと，「\(x(t)\)は2回 \(t\) で微分すると \(F/m\) である」を考えて，この微分方程式を解くと以下の解が得られる．

\[ x(t) = \frac{F}{2m}t^2 \]

また，速度 \(v=\frac{dx}{dt}\) も考える．単純に \(x(t)\) を微分すると以下が得られる．

\[ v=\frac{dx}{dt}=\frac{F}{m}t \]

このように微分方程式から位置，速度，加速度について質量に応じた変化の性質を知ることができる．このようにして物理現象を記述した微分方程式からその現象の性質やダイナミクスを解析することができ，数理解析において微分方程式は重要な概念であることがわかる．

補足

ひょっとすると，位置 \(x(t)\) を時刻 \(t\) で微分したら速度 \(v=\frac{dx}{dt}\)，速度をさらに微分したら加速度 \(a = \frac{d^2x}{dt^2}\) と学んでいるかもしれないが，その場合は加速度 \(a\) で書き換えると上記の式は \(ma=F\) となり見知った方程式になったかもしれない．

Pythonで微分方程式

では，sympyを使ってプログラミングから上記の運動方程式を解く．sympyの詳細な使い方は次回の講義で紹介する．またいくつか勉強に適したsympyの資料を参考資料にまとめておいたのでそちらも参照されたい．

まずは必要なライブラリをimportする．

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, Eq, Derivative, Function, dsolve

数式でのシンボル演算のために次の文字としての変数をsymbols関数で定義する．

m = symbols('m')
t = symbols('t')
F = symbols('F')

続いて，tに依存する関数xをFunctionを使って定義する．

x = Function('x')(t)
x

\[\displaystyle x{\left(t \right)}\]

これまでのpythonと違い変数tに具体的な値を定義していなくても関数xを定義できたことを確認されたい．sympyはこれまで学んだ数学のようにプログラミングすることができ，理論と実装を学ぶ上で非常に便利である．

続いて，速度vを定義する．速度は一階導関数であったので以下のように書ける．微分はDerivativeを利用する．

v = Derivative(x, t)
v

\[\displaystyle \frac{d}{d t} x{\left(t \right)}\]

そして，加速度aを定義する．加速度は二階導関数であったので次のように書く．

a = Derivative(x, t, 2)
a

\[\displaystyle \frac{d^{2}}{d t^{2}} x{\left(t \right)}\]

方程式はEqを利用する．微分方程式を定義できた．

eq = Eq(m * a, F)
eq

\[\displaystyle m \frac{d^{2}}{d t^{2}} x{\left(t \right)} = F\]

微分方程式を解くときは，dsolveを利用する．手計算では二階微分方程式を解くために非常に大変であるが，プログラミングを用いると簡単に解を求められる．sympyを用いた演算は便利であるが，解が正しいかどうか？ を判断するためには，その導出方法を理解する必要がある．あくまでもプログラミングは数式の理解の助けとして利用されたい．

x_ = dsolve(eq, x)
x_

\[\displaystyle x{\left(t \right)} = C_{1} + C_{2} t + \frac{F t^{2}}{2 m}\]

前述した前提条件（厳密には初期条件という）はicsという引数で与えられる．subsは変数に具体的な値を代入するメソッドである．

x_ = dsolve(eq, x, ics={x.subs(t,0): 0, v.subs(t,0): 0})
x_

\[\displaystyle x{\left(t \right)} = \frac{F t^{2}}{2 m}\]

最後に，グラフでプロットする．

from sympy import plotting
plotting.plot(x_.subs(F,1).subs(m,1).rhs, (t, 0, 4))

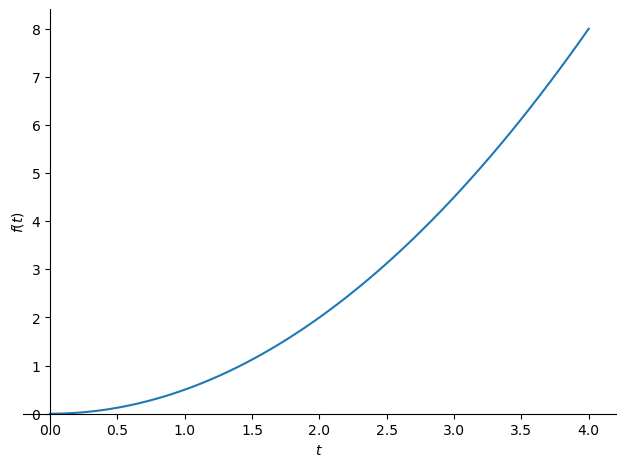
<sympy.plotting.plot.Plot at 0x7fc45956d610>

以上より，微分方程式の解の計算と解のプロットをできた．

フーリエ解析

フーリエ解析 とは，関数を異なる周波数を持つ正弦波の重ね合わせで表現する方法である．フーリエ解析によって，複雑な関数であっても単純な波の組み合わせで表現することで関数の構成要素の性質の理解や分解・合成ができる．前述したように，フーリエ解析によって一般的に解くのが難しい微分方程式を解くのに利用されるだけでなく，波形・音声・動画像・生体信号といった信号処理や解析にも役立つ．

突然だが，関数 \(f(x)\) を \(\sin\)関数と\(\cos\)関数の足し合わせで近似するフーリエ級数を紹介する．詳細や導出は後半の講義で説明する．フーリエ級数は以下で与えられる．

\[ \begin{align} f(x) \sim a_0 + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \end{align} \]

ここで，\(a_0, a_n, b_n\)は以下で与えられる．

\[\begin{split} \begin{align} a_{0}&=\frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx \\ a_{n}&=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx \quad(n=1,2,3 \cdots) \\ b_{n}&=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x d x \quad(n=1,2,3 \cdots) \end{align} \end{split}\]

複雑な式が現れたが，第一回では「関数 \(f(x)\) を \(\sin\)関数と\(\cos\)関数の足し合わせ」で表現することを体感してほしい．係数\(a_0, a_n, b_n\)はひとまず無視して，一番上の式を展開してみると，sin波とcos波の足し算であることがわかる．

\[ f(x) \sim a_0 + a_1 \cos x + b_1 \sin x + a_2 \cos 2x + b_2 \sin 2x + \cdots \]

フーリエ解析（\(\fallingdotseq\)フーリエ級数展開）のポイントは複雑な関数を単純な関数（sin波とcos波）に分解することで複雑な関数の特性を知ることができること，また，単純な関数の組み合わせで複雑な関数を合成することにある．フーリエ解析の導入としてフーリエ級数展開による関数の分解を紹介したが，関数の性質を理解するという意味で数理解析の重要な概念であることがわかってもらえたかと思う．また本講義の後半では，微分方程式への応用のために，フーリエ変換・ラプラス変換を中心に紹介する．

補足: 三角関数系

異なる周波数を持つ三角関数で表される波の集まりとその係数で表現される関数の集合を 三角関数系 と呼び，フーリエ解析を理解する上で非常に重要な概念である．

\[ \{1, \cos x, \sin x, \cos 2x, \sin 2x, \cdots \} \]

Pythonでフーリエ解析

微分方程式と同様にフーリエ級数展開もsympyを用いて計算してみる．今回は例として \(f(x)=x\) という一次関数を用いるが，いろいろな関数を定義してフーリエ級数展開を体験してほしい．

まずは必要なライブラリをimportする．

from sympy import symbols, pi, fourier_series
from sympy.plotting import plot

変数xと関数fを定義する．

x = symbols('x')

f = x
f

\[\displaystyle x\]

グラフにプロットしてみる．

plot(f, xlim=(-pi, pi) , ylim=(-4, 4))

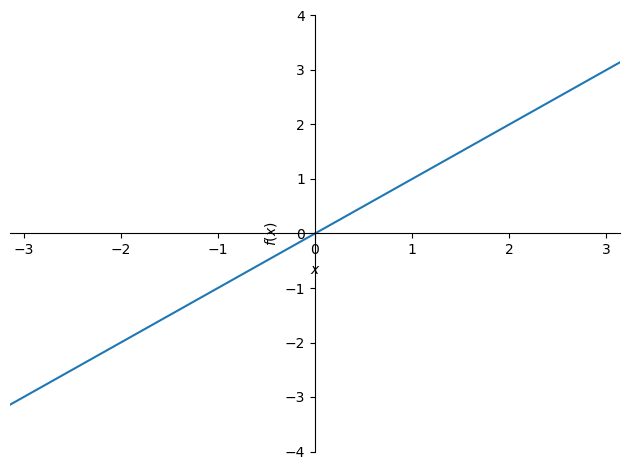
<sympy.plotting.plot.Plot at 0x7fc45974ff10>

sympyではfourier_seriesでフーリエ級数展開できる．関数 f を-piからpiの範囲で展開することを示す．またtruncate()メソッドは何項のsinとcosを使うかを示す．

ff = fourier_series(f, (x, -pi, pi))
ff_8 = ff.truncate(8)
ff_8

\[\displaystyle 2 \sin{\left(x \right)} - \sin{\left(2 x \right)} + \frac{2 \sin{\left(3 x \right)}}{3} - \frac{\sin{\left(4 x \right)}}{2} + \frac{2 \sin{\left(5 x \right)}}{5} - \frac{\sin{\left(6 x \right)}}{3} + \frac{2 \sin{\left(7 x \right)}}{7} - \frac{\sin{\left(8 x \right)}}{4}\]

\(a_{0}=\frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx\)を出力する

ff.a0

\[\displaystyle 0\]

\(a_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx\)を出力する

ff.an

\[\displaystyle \left[0, 0, 0, 0, \ldots\right]\]

\(b_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x d x\)を出力する

ff.bn

\[\displaystyle \left[2 \sin{\left(x \right)}, - \sin{\left(2 x \right)}, \frac{2 \sin{\left(3 x \right)}}{3}, - \frac{\sin{\left(4 x \right)}}{2}, \ldots\right]\]

フーリエ級数展開の結果をプロットしてみる．

p = plot(f, ff_8, xlim=(-pi, pi), ylim=(-4, 4), show=False)
p[1].line_color = 'red'
p.show()

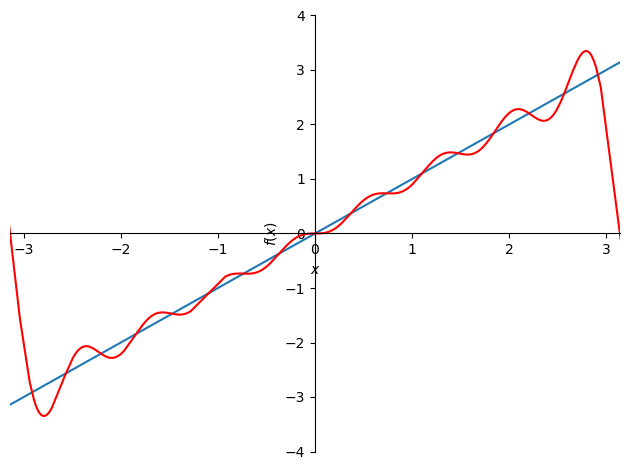
フーリエ級数展開の項数を変更してみる.

ff_1 = fourier_series(f, (x, -pi, pi)).truncate(1)
ff_3 = fourier_series(f, (x, -pi, pi)).truncate(3)
ff_5 = fourier_series(f, (x, -pi, pi)).truncate(5)
ff_11 = fourier_series(f, (x, -pi, pi)).truncate(11)

p = plot(f, ff_1, ff_3, ff_5, ff_11, xlim=(-pi, pi), ylim=(-4, 4), show=False)

N = 5
cm = plt.get_cmap('jet', N)
print(cm, cm.N)
for i in range(cm.N):
    p[i].line_color = cm(i)
p.show()

<matplotlib.colors.LinearSegmentedColormap object at 0x7fc44b0995b0> 5

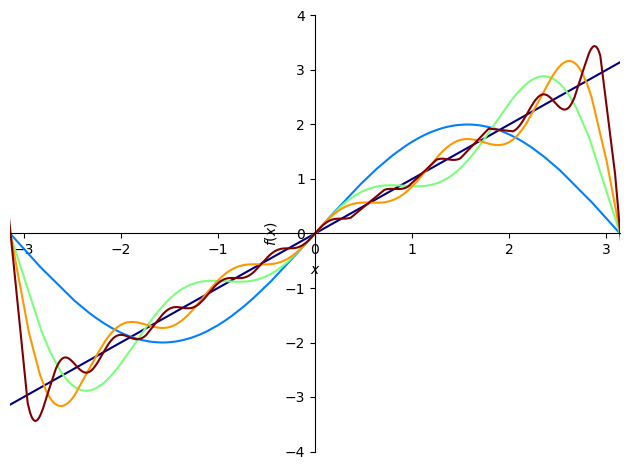
以上より，フーリエ級数の関数の分解を体験できたかと思う．講義後半ではこのように関数を周波数空間で考えることから微分方程式を解く方法を紹介する．またフーリエ解析は微分方程式だけでなく，信号処理においても重要な数学的ツールである．本講義では信号処理的な側面を紹介することはできないが，参考になりそうな書籍を勉強資料にまとめておいたので挑戦されたい．