微分方程式

微分方程式とは？

微分方程式とは，変数 \(x\) と変数 \(x\) を持つ未知関数 \(y\) とその導関数を含む方程式である．例えば，以下のように，

\[ \frac{dy}{dx} = f(x,y) \]

という等式が与えられ，この等式は左辺の独立変数 \(x\) を持つ関数 \(y(x)\) の微分 \(\frac{dy}{dx}\) が右辺の変数 \(x,y\) を持つ関数 \(f(x,y)\) を持つ関数が等しいことを意味し，これまで学んだ \(x=1\) といった解が得られる方程式とは異なり，この等式を満たす関数 \(y(x)\) を求めることが微分方程式を解くということである．

微分方程式の形

微分方程式は大まかに，

1. 関数と導関数が線形性を持つか？

2. 独立変数の数は2つ以上か？ に応じて分類することができる．

線形微分方程式

まず一つ目の「関数と導関数が線形性を持つか？」について，微分方程式を

\[ F(x,y,y')=0 \]

と定義する．ここで\(y'=\frac{dy}{dx}\)であり，実定数 \(\alpha,\beta\)に対して，

\[ \begin{align} F\left(x, \alpha y_1+\beta y_2, \alpha y_1'+\beta y_2'\right)= \alpha F \left(x, y_1, y_1'\right)+\beta F\left(x, y_2, y_2'\right) \end{align} \]

が成立すれば微分方程式が線形であり，その微分方程式を線形微分方程式と呼ぶ．成立しない微分方程式は非線形微分方程式と呼ばれる．非線形微分方程式は簡単にいうと\(y^2\)や\(yy'\)といった非線形項を含む微分方程式と言える．

線形微分方程式の具体例

以下の微分方程式が線形であることを確かめる．

\[ y' - y = x \]

前述の線形性の定義を満たすことを確認すればよいので微分方程式を次のように定義する．

\[ F(x,y,y') = y' - y - x = 0 \]

上式の左辺について，

\[ \begin{align} F\left(x, \alpha y_1+\beta y_2, \alpha y_1'+\beta y_2'\right) &= \alpha y_1' + \beta y_2 ' - (\alpha y_1+\beta y_2) - x \end{align} \]

となる．続いて，右辺について確認する．

\[\begin{split} \begin{align} \alpha F \left(x, y_1, y_1'\right)+\beta F\left(x, y_2, y_2'\right) &= \alpha \left(y_1' - y_1 - x \right) + \beta \left(y_2' - y_2 - x \right) \\ &= \alpha y_1' + \beta y_2' - \alpha y_1 - \beta y_2 - \alpha x - \beta x \\ &= \alpha y_1' + \beta y_2' - \left(\alpha y_1 + \beta y_2\right) - \left(\alpha + \beta\right) x \\ \end{align} \end{split}\]

以上より，\(y,y'\)の項について両辺が一致するので \(y\) について線形であり，これは線形微分方程式である．

非線形微分方程式の具体例

以下の微分方程式が非線形であることを確かめる．

\[ y'' = - y - y^2 \]

前述の線形性の定義を満たすことを確認すればよいので微分方程式を次のように定義する．

\[ F(x,y,y'') = y'' + y + y^2 \]

上式の左辺について，

\[\begin{split} \begin{align} F\left(x, \alpha y_1+\beta y_2, \alpha y_1''+\beta y_2''\right) &= \alpha y_1'' + \beta y_2 '' + \alpha y_1+\beta y_2 + (\alpha y_1)^2 + (\beta y_2)^2 \\ &= \alpha y_1'' + \beta y_2 '' + \alpha y_1+\beta y_2 + \alpha^2 y_1^2 + \beta^2 y_2^2 \end{align} \end{split}\]

となる．続いて，右辺について確認する．

\[\begin{split} \begin{align} \alpha F \left(x, y_1, y_1''\right)+\beta F\left(x, y_2, y_2''\right) &= \alpha \left( y_1'' + y_1 + y_1^2 \right) + \beta \left(y_2'' + y_2 + y_2^2 \right) \\ &= \alpha y_1'' + \beta y_2'' + \alpha y_1 + \beta y_2 + \alpha y_1^2 + \beta y_2^2 \end{align} \end{split}\]

以上より，\(y,y''\)の項について両辺の係数が一致しない．従って，\(y\) について非線形であり，これは非線形微分方程式である．

常微分方程式

続いて，二つ目の「独立変数の数は2つ以上か？」について，一つの独立変数を持つ微分方程式を 常微分方程式（Ordinary Differential Equations, ODEs） と呼び，以下の形で与えられる．

\[ \begin{align} F\left(x, y, y',..., y^{(n)}\right) =F\left(x, y, \frac{dy}{dx},...,\frac{d^ny}{dx^n}\right)=0 \end{align} \]

このとき，復習であるが\(y^{(n)}\)は\(n\)階の導関数であり，微分方程式に含まれる導関数の最大の次数 \(n\) を微分方程式の階数と呼ぶ．上記の式には一つの独立変数 \(x\) と関数\(y(x)\)，またその導関数 \(\{y',...y^{n}\}\)が含まれている．

偏微分方程式

常微分方程式とは異なり，二つ以上の独立変数を持つ微分方程式を 偏微分方程式（Partial Differential Equations, PDEs） と呼ぶ．偏微分方程式は関数の偏微分に関する等式であり，以下で与えられる．

\[ \begin{align} F\left(x_1, x_2, ..., x_n, u, \frac{\partial u}{\partial x_1}, \frac{\partial u}{\partial x_2}, ..., \frac{\partial u}{\partial x_n}, \frac{\partial^2 u}{\partial x_1^2}, \frac{\partial^2 u}{\partial x_2^2}, ..., \frac{\partial^2 u}{\partial x_n^2}, ...\right) = 0 \end{align} \]

ここで，\(F\)はある関数，\(x_1, x_2, ..., x_n\)は\(n\)個の独立変数，関数\(u\)は求める未知関数を表す．また，\(\frac{\partial u}{\partial x_i}\)は\(u\)の\(x_i\)に対する一階の偏微分を表し，\(n\)階の偏微分を含む．常微分方程式とは異なり，複数個の独立変数とその偏導関数が含まれていることを確認されたい．

微分方程式の例

具体例から微分方程式を理解しよう．関数 \(f(x,y)\) が \(f(x,y)=x\) であるときを考える．この関数は一階の常微分方程式として分類される．

\[ \frac{dy}{dx} = x \]

この微分方程式は，関数 \(y(x)\) の導関数が関数 \(x\) と等しいことを意味する．初めは，慣れないが，微分したら \(x\) となるような関数を求めることがゴールであり，このような関数は容易に暗算で計算できる．

\[ y(x) = \frac{x^2}{2} + C \]

このとき，\(C\)は積分定数であり，上記の関数 \(y(x)\) を微分 \(\frac{dy}{dx}\) すると \(x\)となることがわかるかと思う．この解は任意の定数 \(C\) に対する解の集合を表しており，これを一般解と呼ぶ．

では上記の微分方程式をsympyで解いてみる．まずは必要なライブラリをimportする．

from sympy import symbols, Eq, Derivative, Function, dsolve

変数 x と関数 y(x) を定義する．

x = symbols('x')
y = Function('y')(x)
y

\[\displaystyle y{\left(x \right)}\]

y(x) を x で微分した \(dy/dx\) を作成する．

dy = Derivative(y, x)
dy

\[\displaystyle \frac{d}{d x} y{\left(x \right)}\]

Eq を使って方程式を定義する．

eq = Eq(dy, x)
eq

\[\displaystyle \frac{d}{d x} y{\left(x \right)} = x\]

dsolve関数を使って未知関数 y(x) を求める．

y_ = dsolve(eq, y)
y_

\[\displaystyle y{\left(x \right)} = C_{1} + \frac{x^{2}}{2}\]

手計算の結果と一致することを確認されたい．

一般解と特殊解

改めて前述の話をまとめる．微分方程式は解として未知関数を持つ方程式であり，上記のように，積分定数を含む形で解の集合を表す形式を一般解と言った．ここでの解の集合は任意の定数 \(C\) は微分して消えるのでどのような値が入っていもいいと考えると，導出した解は，例えば，\(y(x) = x^2/2\), \(y(x) = x^2/2 + 1\) などさまざまな関数を解として持つことがわかる．つまり，一般解はパラメータ \(C\) を持つ関数の集合なのである．

では，これをsympyを使ってプロットしてみよう．

from sympy import plotting
plotting.plot(
    y_.rhs.subs(symbols('C1'), -3),
    y_.rhs.subs(symbols('C1'), -2),
    y_.rhs.subs(symbols('C1'), -1),
    y_.rhs.subs(symbols('C1'), 0),
    y_.rhs.subs(symbols('C1'), 1),
    y_.rhs.subs(symbols('C1'), 2),
    y_.rhs.subs(symbols('C1'), 3), (x, -2, 2))

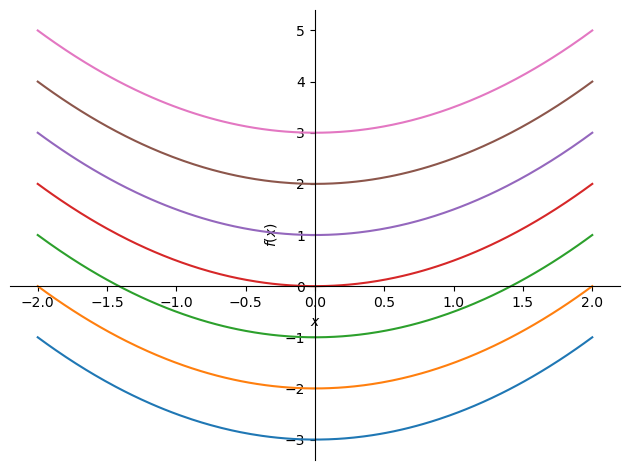
<sympy.plotting.plot.Plot at 0x7fcbf9295b20>

上記のように，積分定数 C1 に値を入力してみると，複数の解の候補がプロットできる．これが一般解であり，解の集合（=関数の集合）ということである．

そして，第一回の講義で紹介したように，問題によっては解に条件が課される場合がある．その条件を 初期条件 と呼び，初期条件に基づいて上記の集合からある特定の解（関数）を求めることができる．このときの解を 特殊解 という．

前述の例に初期条件を付加すると，

\[ \frac{dy}{dx} = x, \quad y(0) = 1 \]

となる．これはつまり，\(x=0\) のときの未知関数 \(y\) の値は \(1\) であるという初期条件である．一般解が以下であったので，

\[ y(x) = \frac{x^2}{2} + C \]

この一般解に \(y(0) = 1\) を代入する．

\[\begin{split} \begin{align} y(0) &= \frac{0^2}{2} + C \\ 1 &= 0 + C \\ C &= 1 \end{align} \end{split}\]

となり，積分定数 \(C\) は \(1\) であり，特殊解は

\[ y(x) = \frac{x^2}{2} + 1 \]

である．

sympyのdsolveに初期条件を与えて特殊解を計算するためには，icsというキーワード引数で辞書形式で初期条件を与えれば良い．

y_ = dsolve(eq, y, ics={y.subs(x,0): 1})
y_

\[\displaystyle y{\left(x \right)} = \frac{x^{2}}{2} + 1\]

これをプロットすると以下となる．

plotting.plot(y_.rhs, (x, -2, 2))

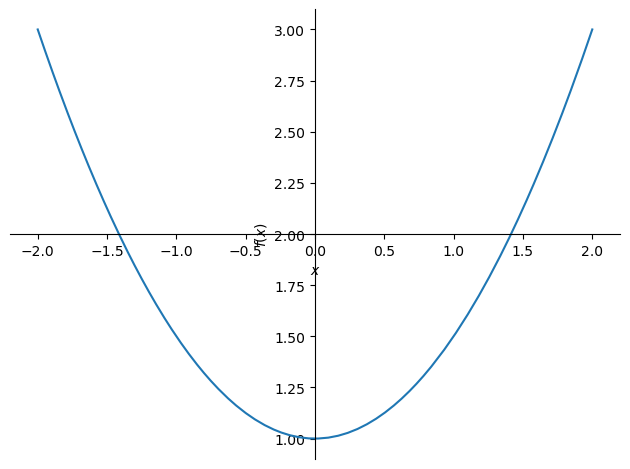
<sympy.plotting.plot.Plot at 0x7fcbeaa9a340>