二階定数係数線形同次微分方程式

二階線形微分方程式

二階線形微分方程式 は以下のように2階の導関数を持つ微分方程式である．

\[ \frac{d^2y}{dx^2} + p(x)\frac{dy}{dx} + q(x)y = g(x) \]

ここで，\(p(x)\)，\(q(x)\)，\(g(x)\)は\(x\)の関数である．一階の線形微分方程式で扱ったように，\(g(x)\)が恒等的に0であるときは二階線形同次微分方程式と呼ばれ，0でないときは二階線形非同次微分方程式と呼ばれる．

二階線形同次微分方程式

前述したように二階線形同次微分方程式は以下の形で表される微分方程式である．

\[ \frac{d^2y}{dx^2} + p(x)\frac{dy}{dx} + q(x)y = 0 \]

ここで，\(p(x),q(x),g(x)\)は\(x\)の関数である．同次微分方程式であるので右辺が0であることを確認されたい．

解法

二階線形同次微分方程式には2つの一次独立な 基本解 \(y_1,y_2\)が存在し，これらを重ね合わせた一般解 \(y\) は以下のようになることが知られている．

\[ y=C_1y_1 + C_2y_2 \]

\(C_1,C_2\)は積分定数であり，この一般解は基本解 \(y_1,y_2\) の線型結合であることがわかる．これは微分方程式の線形性から得られる性質（重ね合わせの原理）である．

しかしながら，このような基本解は一般的に求めることができない．ここでは，\(p(x),q(x)\)が定数であるときの二階定数係数線形微分方程式についてのみ紹介する．

二階定数係数線形同次微分方程式

各導関数が定数係数を持つ場合の 二階定数係数線形同次微分方程式 は次の形式で書かれる微分方程式である．

\[ \frac{d^2y}{dx^2} + a\frac{dy}{dx} + by = 0 \]

ただし，\(a,b\)は定数である．

解法

この微分方程式の解は特性方程式と呼ばれる形から求める．具体的に，一階の線形同次微分方程式の一般解が \(y(x)= C e^{-\int p(x) dx}\) であったことから，二階の微分方程式の階も似た解の形を持つと考える．そこで，以下のように解を

\[ y=e^{\lambda x} \]

と仮定する．では，このように仮定したとき，どのような \(\lambda\) であれば微分方程式の解になるかを考える．そのために，この仮定の解を与えられた二階定数係数線形同次微分方程式へ代入する

\[\begin{split} \begin{aligned} \frac{d^2}{dx^2} e^{\lambda x} + a\frac{d}{dx} e^{\lambda x} + b e^{\lambda x} &= 0 \\ \lambda^2 e^{\lambda x} + a\lambda e^{\lambda x} + b e^{\lambda x} &= 0 \\ \left ( \lambda^2 + a \lambda + b \right ) e^{\lambda x} &= 0 \end{aligned} \end{split}\]

以上の方程式が得られ，\(e^{\lambda x} \neq 0\) よりこの等式が満たされる条件は以下となる．

\[ \lambda^2 + a \lambda + b = 0 \]

この二次方程式は 特性方程式 と呼ばれ，この方程式を満たすような \(\lambda\) を考えれば良い．つまり，二次方程式の解で学んだように，二階定数係数線形同次微分方程式の一般解は上記の二次方程式の判別式，

\[ D=a^2 - 4b \]

で判別することができる．では，場合分けを行う．

1. \(D=a^2 - 4b > 0\)

このとき，特性方程式は二つの異なる実根 \(\lambda_{\alpha}, \lambda_{\beta}\) を持ち，その一般解は以下となる．

\[ y = C_1 e^{\lambda_{\alpha}x} + C_2 e^{\lambda_{\beta}x} \]

2. \(D=a^2 - 4b = 0\)

このとき，特性方程式は重根 \(\lambda_{\alpha} = \lambda_{\beta} = \frac{-a}{2}\)を持ち，その一般解は以下となる．

\[ y = \left ( C_1 x + C_2\right )e^{\lambda_{\alpha}x} \]

3. \(D=a^2 - 4b < 0\)

このとき，特性方程式は複素共役な解 \(\lambda_{\alpha}=p+qi, \lambda_{\beta}=p-qi\) を持ち，その一般解は以下となる．

\[ y=e^{px} \left( C_1 \cos qx + C_2 \sin qx \right) \]

このとき，\(C_1,C_2\)は積分定数であり，\(i\) は虚数単位，\(p,q\)は0以外の実数である．

具体例（二つの異なる実根の場合）

では，次の同次微分方程式を解いてみよう．

\[ \frac{d^2y}{dx^2} + 3\frac{dy}{dx} + 2y = 0 \]

解答はクリックで確認できる．

与えられた二階微分方程式の一般解を \(y=e^{\lambda x}\) とおく．特性方程式を考えると，

\[\begin{split} \begin{aligned} \frac{d^2}{dx^2} e^{\lambda x} + 3 \frac{d}{dx} e^{\lambda x} + 2 e^{\lambda x} &= 0 \\ \lambda^2 e^{\lambda x} + 3 \lambda e^{\lambda x} + 2 e^{\lambda x} &= 0 \\ \left ( \lambda^2 + 3 \lambda + 2 \right ) e^{\lambda x} &= 0 \end{aligned} \end{split}\]

以上の方程式が得られ，\(e^{\lambda x} \neq 0\) よりこの等式が満たされる条件は以下となる．

\[ \lambda^2 + 3 \lambda + 2 = 0 \]

この方程式を \(\lambda\) について解くと，

\[ \lambda^2 + 3 \lambda + 2 = \left( \lambda + 1 \right)\left( \lambda + 2 \right) = 0 \]

より，

\[ \lambda = -1, -2 \]

であり，特性方程式は二つの異なる解を持つので，一般解は

\[ y = C_1 e^{-x} + C_2 e^{-2x} \]

となる．

具体例（重根の場合）

では，次の同次微分方程式を解いてみよう．

\[ \frac{d^2y}{dx^2} -2\frac{dy}{dx} + y = 0 \]

解答はクリックで確認できる．

与えられた微分方程式について，一般解を \(y=e^{\lambda x}\) としたときの特性方程式を考える．特性方程式は，

\[ \lambda^2 -2 \lambda + 1 = 0 \]

より，

\[ \lambda = 1 \]

の重根であった．したがって一般解は以下となる．

\[ y = \left ( C_1 x + C_2\right )e^{x} \]

具体例（複素共役な解の場合）

では，次の同次微分方程式を解いてみよう．

\[ \frac{d^2y}{dx^2} + 2\frac{dy}{dx} + 2y = 0 \]

解答はクリックで確認できる．

与えられた微分方程式について，一般解を \(y=e^{\lambda x}\) としたときの特性方程式を考える．特性方程式は，

\[ \lambda^2 + 2 \lambda + 2 = 0 \]

より，

\[ \lambda = -1 \pm i \]

であり共役な複素数解を持つ．したがって一般解は以下となる．

\[ y = e^{-x} \left( C_1 \cos x + C_2 \sin x \right) \]

Pythonによる実装

では，具体例（二つの異なる実根の場合）をsympyで解く．

from sympy import symbols, Eq, Derivative, Function, dsolve

# 変数と未知関数の定義
x = symbols('x')
y = Function('y')(x)

# dy/dxの定義
dy = Derivative(y, x)
dy2 = Derivative(y, x, 2)

# 微分方程式の定義
eq = Eq(dy2 + 3*dy + 2*y, 0)

# 微分方程式を解く
y_ = dsolve(eq, y)
y_

\[\displaystyle y{\left(x \right)} = \left(C_{1} + C_{2} e^{- x}\right) e^{- x}\]

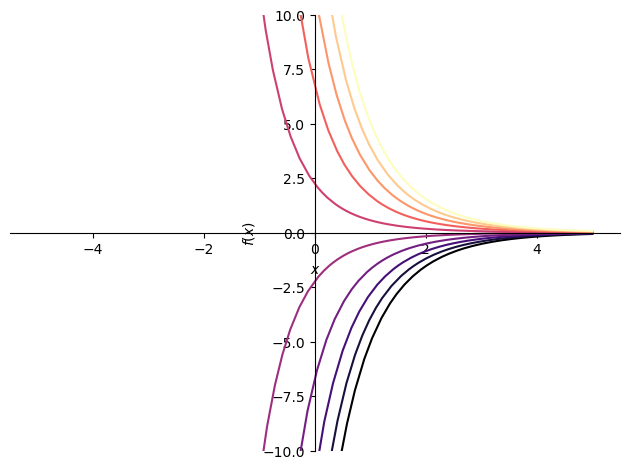
これをプロットしてみる．ただし，\(C_1 = C_2\) として値を代入している．

import numpy as np
from sympy import plotting
import matplotlib.pyplot as plt

N = 10

eqs = []
for c in np.linspace(-10, 10, N):
    eqs.append(y_.rhs.subs(symbols('C1'), c).subs(symbols('C2'), c))
p = plotting.plot(*eqs, (x, -5, 5), ylim=(-10, 10), show=False)

cm = plt.get_cmap('magma', N)
for i in range(N):
    p[i].line_color = cm(i)
p.show()