複素フーリエ級数展開

フーリエ級数展開は，区間 \(-T/2 \leq t \leq T/2\) 上の関数 \(f(t)\) を基本周波数 \(\omega_0\) の整数倍の周波数の正弦波の重ね合わせで表現することであった．そして，そのときのフーリエ級数とフーリエ係数は以下であった．

\[ \begin{align} f(t) &\approx \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \cos k \omega_0 t + b_k \sin k \omega_0 t), \quad -\frac{T}{2} \leq t \leq \frac{T}{2} \end{align} \]

\[ a_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt, \quad b_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \]

ここでは，上記のフーリエ級数と係数を以下の三角関数の指数関数表記で書き換えることを試みる．

\[ \begin{align} \cos \theta = \frac{e^{i\theta}+e^{-i\theta}}{2}, \quad \sin \theta = \frac{e^{i\theta}-e^{-i\theta}}{2i} \end{align} \]

ここで \(i\) は虚数単位である．上記の\(\sin\)関数と\(\cos\)関数の指数関数表記は オイラーの公式 から導出でき，これらを用いて書き換えるとフーリエ級数は以下となる．

\[ \begin{align} f(t) = \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \end{align} \]

\[ C_k = \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \]

ここで第一式を 複素フーリエ級数 といい，第二式を 複素フーリエ係数 という．この複素フーリエ級数と係数の導出を行う．

複素数

虚数と複素数について簡単に復習する．虚数 \(i\) は二乗すると \(-1\) となる数であり，以下で定義されていた．

\[ i^2 = -1 \]

複素数は二つの実数 \(a,b\) と虚数 \(i\) を用いて \(a+bi\) の形で表される数であった．このとき，\(b=0\) ならば \(a+bi\) は実数であり，\(b \neq 0\) ならば\(b=0\) ならば \(a+bi\) は虚数であった．

そして，複素数も実数と同様に等価や四則演算について考えることができた．二つの複素数 \(a+bi\) と \(c+di\) が 等しい とは，\(a=c, b=d\) ならばこれらの複素数が等しいという．複素数の四則演算については以下のようになっている．

• 加法

  \[ \left ( a + bi \right ) + \left ( c + di \right ) = \left ( a + c \right ) + \left ( b + d \right )i \]

• 減法

  \[ \left ( a + bi \right ) - \left ( c + di \right ) = \left ( a - c \right ) + \left ( b - d \right )i \]

• 乗法

  \[ \left ( a + bi \right ) \left ( c + di \right ) = \left ( ac - bd \right ) + \left ( ad + bc \right )i \]

• 除法

  \[ \frac{a+bi}{c+di} = \frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i \]

共役な複素数

共役な複素数 とは虚部の符号を反転した複素数である．複素数 \(\alpha=a+bi\) の共役な複素数 \(\bar{\alpha}\) は以下である．

\[ \bar{\alpha} = a-bi \]

そして，共役な複素数は以下のような性質を持っている．

• 和に関する性質

  \[ \alpha + \bar{\alpha} = 2a \]

• 積に関する性質

  \[ \alpha \bar{\alpha} = a^2+b^2 \]

• 共役な複素数の計算

  \[ \overline{\alpha \pm \beta} = \overline{\alpha} \pm \overline{\beta} \]
  \[ \overline{\alpha\beta} = \overline{\alpha}\overline{\beta} \]
  \[ \overline{\left(\frac{\alpha}{\beta}\right )} = \frac{\overline{\alpha}}{\overline{\beta}} \]

複素平面

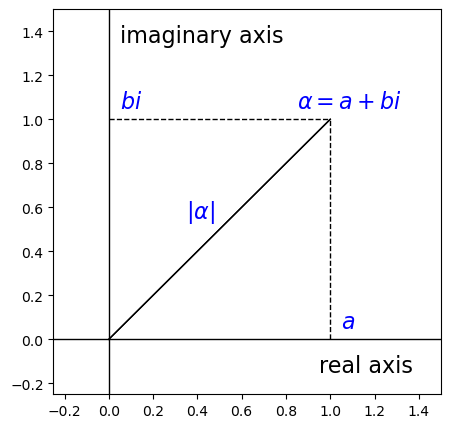
実数の場合と同様に複素数 \(\alpha=a+bi\) について実数 \(a\) に関する 実軸 と虚数 \(b\) に関する 虚軸 を用いて座標平面上の点 \((a,b)\) に関する平面を描くことができる．これを 複素平面 という．

このとき，原点から点 \((a,b)\) までの距離として，複素数 \(\alpha=a+bi\) に対して \(\sqrt{a^2+b^2}\) を \(\alpha\) の絶対値 \(|\alpha|\) で定義する．

\[ |\alpha| = |a+bi| = \sqrt{a^2+b^2} \]

import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))

px, py = 1, 1
pad = 0.05

ax.plot([-0.5,2],[0,0], color="k", linewidth=1)
ax.plot([0,0],[-0.5,2], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([px,px],[0,py], color="k", linewidth=1, linestyle="--")
ax.plot([0,px],[py,py], color="k", linewidth=1, linestyle="--")

ax.text(pad, 1.3 + pad, r"imaginary axis", color="k", fontsize=16)
ax.text(pad, 1.0 + pad, r"$bi$", color="b", fontsize=16)

ax.text(pad + 0.9, pad - 0.2, r"real axis", color="k", fontsize=16)
ax.text(pad + 1.0, pad, r"$a$", color="b", fontsize=16)

ax.text(pad + 0.8, pad + 1.0, r"$\alpha=a+bi$", color="b", fontsize=16)
ax.text(pad + 0.3, pad + 0.5, r"$|\alpha|$", color="b", fontsize=16)

ax.set_xlim(-0.25, 1.5)
ax.set_ylim(-0.25, 1.5)

(-0.25, 1.5)

オイラーの公式

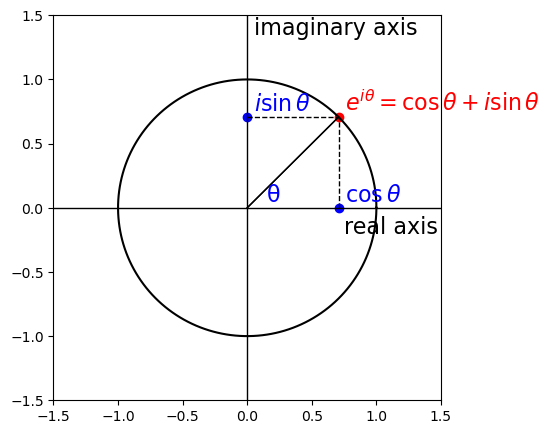
オイラーの公式 とは，虚数単位 \(i\) を使った指数関数 \(e^{i\theta}\) と \(\sin \theta, \cos \theta\) との関係式である．これは以下で示される．

\[ e^{i\theta} = \cos \theta + i \sin \theta \]

オイラーの公式を幾何学的に解釈すると \(e^{i\theta}\) は複素平面の単位円上の実軸からの角度 \(\theta\) の点を示している．

この回転角 \(\theta\) は 偏角 という．

import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))
theta = np.linspace(0, 2*np.pi, 360)
x = np.cos(theta)
y = np.sin(theta)

deg = 45
px = np.cos(np.deg2rad(deg))
py = np.sin(np.deg2rad(deg))

pad = 0.05
ax.scatter(px, py, c="r")
ax.text(px+pad, py+pad, r"$e^{i\theta} = \cos \theta + i \sin \theta$", color="r", fontsize=16)

ax.scatter(px, 0, c="b")
ax.text(px+pad, pad, r"$\cos \theta$", color="b", fontsize=16)

ax.scatter(0, py, c="b")
ax.text(pad, py+pad, r"$i \sin \theta$", color="b", fontsize=16)

ax.plot([-2,2],[0,0], color="k", linewidth=1)
ax.plot([0,0],[-2,2], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([px,px],[0,py], color="k", linewidth=1, linestyle="--")
ax.plot([0,px],[py,py], color="k", linewidth=1, linestyle="--")

ax.text(pad, 1.3 + pad, r"imaginary axis", color="k", fontsize=16)
ax.text(pad + 0.7, pad - 0.25, r"real axis", color="k", fontsize=16)
ax.text(pad+0.1, pad, "θ", color="b", fontsize=16)

ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.plot(x, y, color='k')

[<matplotlib.lines.Line2D at 0x7fa25a5bd4c0>]

そして，オイラーの公式を使うと任意の複素数 \(z=a+bi\) は偏角 \(\theta\) と原点からの距離 \(r\) を使って \(r (\cos \theta + i \sin \theta)\) と書ける．

\[\begin{split} \begin{align} z &= a+bi \\ &= r \left ( \cos \theta + i \sin \theta \right ) \\ &= re^{i\theta} \end{align} \end{split}\]

三角関数の定義と実軸・虚軸に注意すればこの表記となることは明らかである．

Pythonによる複素数の定義

sympyは複素数も扱うことができる．虚数単位 \(i\) は from sympy import I で導入できる．

from sympy import I
I

\[\displaystyle i\]

複素数は以下のように定義する．

z1 = 2 + 3*I
z1

\[\displaystyle 2 + 3 i\]

共役な複素数は .conjugate() で取得できる．

z1.conjugate()

\[\displaystyle 2 - 3 i\]

実部と虚部はそれぞれreとimで取得できる．

from sympy import re, im
re(z1)

\[\displaystyle 2\]

im(z1)

\[\displaystyle 3\]

三角関数の指数表記

複素数の話題を深掘りすると説明すべきことは数多くあるが，本講義で説明する複素フーリエ級数と係数の導出に必要な情報は以上である（より詳しく勉強したい人は複素解析あたりを調べてみるといいと思います）．まずはオイラーの公式を使って三角関数を指数関数表記

\[ \begin{align} \cos \theta = \frac{e^{i\theta}+e^{-i\theta}}{2}, \quad \sin \theta = \frac{e^{i\theta}-e^{-i\theta}}{2i} \end{align} \]

に書き換える．これは以下のように導出できる．まず \(\theta, -\theta\) に関するオイラーの公式を考える．

\[ e^{i\theta} = \cos \theta + i \sin \theta, \quad e^{-i\theta} = \cos \theta - i \sin \theta \]

そして，\(\cos \theta\) について \(e^{i\theta}\) と \(e^{-i\theta}\) の和を考えると \(\sin\) 関数の項が消えるので以下のように整理する．

\[\begin{split} \begin{align} e^{i\theta} + e^{-i\theta} &= \cos \theta + i \sin \theta + \cos \theta - i \sin \theta \\ e^{i\theta} + e^{-i\theta} &= 2 \cos \theta \\ \cos \theta &= \frac{e^{i\theta} + e^{-i\theta}}{2} \end{align} \end{split}\]

同様にして，\(\sin \theta\) については \(e^{i\theta}\) と \(e^{-i\theta}\) の差を考えればよい．

\[\begin{split} \begin{align} e^{i\theta} - e^{-i\theta} &= \cos \theta + i \sin \theta - \cos \theta + i \sin \theta \\ e^{i\theta} - e^{-i\theta} &= 2i \sin \theta \\ \sin \theta &= \frac{e^{i\theta} - e^{-i\theta}}{2i} \end{align} \end{split}\]

以上より，三角関数の指数表記を導出できた．

オイラーの公式と三角関数の加法定理

補足となるが，オイラーの公式から三角関数の加法定理や倍角の公式の関連を導出できる．高校数学で学んだ加法定理は以下であった．

\[\begin{split} \begin{align} \cos \left ( \alpha + \beta \right ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \sin \left ( \alpha + \beta \right ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{align} \end{split}\]

これらの式を \(\theta = \alpha + \beta\) としてオイラーの公式から考えると，

\[ e^{i \left (\alpha+\beta \right )} = \cos \left (\alpha+\beta \right ) + i \sin \left (\alpha+\beta \right ) \]

となる．実部と虚部に加法定理の \(\cos \left ( \alpha + \beta \right )\) と \(\sin \left ( \alpha + \beta \right )\) が含まれていることがわかる． オイラーの公式に当てはめるのではなく，\(e^{i \left (\alpha+\beta \right )}\)について指数関数の性質に注意して式変形してみると

\[\begin{split} \begin{align} e^{i \left (\alpha+\beta \right )} &= e^{i \alpha + i \beta} \\ &= e^{i \alpha}e^{i \beta} \\ &= \left ( \cos \alpha + i \sin \alpha \right ) \left ( \cos \beta + i \sin \beta \right ) \\ &= \left ( \cos \alpha \cos \beta - \sin \alpha \sin \beta\right ) + i \left ( \sin \alpha \cos \beta + \cos \alpha \sin \beta \right ) \end{align} \end{split}\]

となり，加法定理の結果が実部と虚部に現れる．同様にして指数関数の冪乗の性質

\[ \left ( e^{i\theta} \right )^n = e^{in\theta} \]

を使うと倍角公式も導出できる．

複素フーリエ級数と係数の導出

では，三角関数の指数関数表記を利用して実数のフーリエ級数展開から複素フーリエ級数展開を導出する．まずフーリエ級数展開の式から整理していく．三角関数の指数関数表記

\[ \begin{align} \cos \theta = \frac{e^{i\theta}+e^{-i\theta}}{2}, \quad \sin \theta = \frac{e^{i\theta}-e^{-i\theta}}{2i} \end{align} \]

を使って，フーリエ級数展開に含まれる \(\cos\) 関数と \(\sin\) 関数を書き換える．

\[\begin{split} \begin{align} f(t) &= \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \cos k \omega_0 t + b_k \sin k \omega_0 t) \\ &= \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \frac{e^{ik \omega_0 t}+e^{-ik \omega_0 t}}{2} + b_k \frac{e^{ik \omega_0 t}-e^{-ik \omega_0 t}}{2i}) \\ &= \frac{a_{0}}{2} + \sum_{k=1}^{\infty} \frac{\left ( a_k e^{ik \omega_0 t} + a_k e^{-ik \omega_0 t} - i b_k e^{ik \omega_0 t} + i b_k e^{-ik \omega_0 t} \right )}{2} \\ &= \frac{a_{0}}{2} + \sum_{k=1}^{\infty} \left ( \frac{a_k - i b_k}{2} e^{ik \omega_0 t} + \frac{ a_k + i b_k}{2} e^{-ik \omega_0 t}\right ) \end{align} \end{split}\]

\(\cos\) 関数と \(\sin\) 関数は \(e^{i\theta}\) に関する項に変換できた．次は，フーリエ係数 \(a_0, a_k, b_k\) の整理である．ここで式をみると，\(C_0 = \frac{a_{0}}{2}, C_k = \frac{a_k - i b_k}{2}, C_{-k}=\frac{ a_k + i b_k}{2}\) として複素フーリエ係数を考えると式をまとめることができることがわかる．フーリエ係数 \(a_0, a_k, b_k\) は以下であったので

\[ a_0 = \frac{2}{T} \int_{-T/2}^{T/2} f(t) dt, \quad a_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt, \quad b_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \]

これらに注意して定義した \(C_0, C_k, C_{-k}\) の導出を行う．

\[\begin{split} C_k = \begin{cases} \left (a_k - ib_k \right ) / 2 & k > 0 \\ a_0 / 2 & k = 0 \\ \left (a_{-k} + ib_{-k} \right ) / 2 & k < 0 \end{cases} \end{split}\]

まず \(C_0\) の式変形について以下のように整理できる．

\[\begin{split} \begin{align} C_0 &= \frac{a_{0}}{2} \\ &= \frac{1}{2} \frac{2}{T} \int_{-T/2}^{T/2} f(t) dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) dt \end{align} \end{split}\]

続いて，\(C_k\) は以下のように式変形する．

\[\begin{split} \begin{align} C_k &= \frac{a_k - i b_k}{2} \\ &= \frac{1}{2}\frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt - \frac{i}{2} \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt - \frac{i}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) \left ( \cos k \omega_0 t - i \sin k \omega_0 t \right ) dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) e^{-ik \omega_0 t} dt \end{align} \end{split}\]

最後に \(C_{-k}\) は以下となる．

\[\begin{split} \begin{align} C_{-k} &= \frac{a_k + i b_k}{2} \\ &= \frac{1}{2}\frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt + \frac{i}{2} \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt + \frac{i}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) \left ( \cos k \omega_0 t + i \sin k \omega_0 t \right ) dt \\ &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) e^{ik \omega_0 t} dt \end{align} \end{split}\]

以上より，フーリエ係数を書き換えることができた．またこのように表記することで，\(k=0,k>0,k<0\) の条件で場合分けすると各係数を単一の \(C_k\) で表現でき，フーリエ級数展開をよりシンプルに書くことができる．

まとめると，複素フーリエ級数は区間 \(-T/2 \leq t \leq T/2\) 上の関数 \(f(t)\) を基本周波数 \(\omega_0\) の整数倍の周波数を持つ虚数 \(i\) を含む指数関数表記された正弦波の重ね合わせで表現する方法である．複素フーリエ級数と複素フーリエ係数は以下である．

\[ \begin{align} f(t) = \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \end{align} \]

\[ C_k = \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \]

複素数で書き換えたが \(e^{ik\omega_0 t}\) は波を表すので中身はフーリエ級数展開と同じであることに注意されたい（オイラーの公式からも明らかだと思う）．また \(C_k\) は スペクトル とも呼ばれる．

具体例

では，区間 \([-\pi, \pi]\) 上の以下の関数 \(f(t)\) について複素フーリエ級数展開してみよう．

\[\begin{split} f(t) = \begin{cases} 1 & -\pi < t \leq 0 \\ 0 & 0 < t \leq \pi \end{cases} \end{split}\]

解答はクリックで確認できる．

複素フーリエ係数 \(C_0,C_k\) を計算する．まず \(\omega_0 = 2 \pi / T\) で周期 \(T = 2\pi\) より基本周波数は \(\omega_0 = 1\) であることがわかる．これより複素フーリエ係数 \(C_0\) を上記で導出した複素フーリエ係数の式から計算する．

\(C_0(k=0)\)のとき

\[\begin{split} \begin{align} C_0 &= \frac{1}{2\pi}\int^{\pi}_{-\pi} f\left ( t \right ) e^{-i\cdot 0 \cdot t} dt \\ &= \frac{1}{2\pi}\int^{\pi}_{-\pi} f\left ( t \right ) dt \\ &= \frac{1}{2\pi} \left\{ \int_{-\pi}^{0} 1 dt + \int_{0}^{\pi} 0 dt \right\} \\ &= \frac{1}{2\pi} \left [ t \right ]^{0}_{-\pi} \\ &= \frac{1}{2\pi} \left \{ 0 + \pi \right \} = \frac{1}{2} \end{align} \end{split}\]

続いて，\(C_k(k \neq 0)\)のとき

\[\begin{split} \begin{align} C_k &= \frac{1}{T}\int^{T/2}_{-T/2} f\left ( t \right ) e^{-ik\omega_0 t} dt \\ &= \frac{1}{2\pi}\int^{\pi}_{-\pi} f\left ( t \right ) e^{-ikt} dt \\ &= \frac{1}{2\pi}\left\{ \int_{-\pi}^{0} 1 e^{-ikt} dt + \int_{0}^{\pi} 0 e^{-ikt} dt \right\} \\ &= \frac{1}{2\pi}\left [ \frac{1}{-ik} e^{-ikt} \right ]^{0}_{-\pi} \\ &= \frac{1}{2\pi}\left ( \frac{1}{-ik} e^{-ik \cdot 0} - \frac{1}{-ik} e^{-ik \cdot -\pi} \right ) \\ &= \frac{1}{2\pi}\left ( \frac{1}{-ik} + \frac{1}{ik} e^{ik\pi} \right ) \\ &= \frac{1}{2\pi}\left ( \frac{1 - e^{ik\pi}}{-ik} \right ) \\ &= \frac{1}{2\pi}\left ( \frac{1 - \cos k\pi - i \sin k\pi}{-ik} \right ) \\ &= \frac{1}{2\pi}\left \{ \frac{1 - \left ( -1 \right )^k}{-ik} \right \} \\ &= - \frac{1}{2ik\pi}\left \{ 1 - \left ( -1 \right )^k \right \} \\ &= \frac{i}{2k\pi}\left \{ 1 - \left ( -1 \right )^k \right \} \\ \end{align} \end{split}\]

以上より，複素フーリエ級数が以下のように計算された．

\[ C_0 = \frac{1}{2}, \quad C_k = \frac{i}{2k\pi}\left \{ 1 - \left ( -1 \right )^k \right \} \]

よって複素フーリエ級数の式に代入すると

\[ f(t) = \frac{1}{2} + \frac{i}{2\pi}\sum_{k=\pm 1}^{\pm\infty} \frac{1 - \left ( -1 \right )^k} {k} e^{ikt} \]

となる．

Pythonで複素フーリエ級数展開

では，前述した複素フーリエ級数展開をsympyで実装する．まずは近似対象の関数を定義する．

from sympy import symbols
t = symbols('t')
f = t**2
f

\[\displaystyle t^{2}\]

from sympy import pi
from sympy.plotting import plot
plot(f, xlim=(-pi, pi) , ylim=(-5, 5))

<sympy.plotting.plot.Plot at 0x7fa25a63ecd0>

複素フーリエ係数 \(C_k\) を定義する．

from sympy import Integral, exp
k = symbols('k')
T = 2 * pi # 周期 T = 2π
omega_0 = 2 * pi / T # 基本周波数

c_k = Integral(f * exp(-k * I * omega_0 * t), (t, -T/2, T/2)) / T
c_k

\[\displaystyle \frac{\int\limits_{- \pi}^{\pi} t^{2} e^{- i k t}\, dt}{2 \pi}\]

複素フーリエ級数を計算する．前回の講義と同様に，\(k\)番目の項と周期\(T\)を変数として定義していたのでsubs()で代入し，上記で定義した\(a_k,b_k\)の積分を.doit()で実行する．今回は \(C_{-1}, C_0, C_1\) の三項のみで近似する．

c_m1 = c_k.subs(k, -1).doit()
c_m1

\[\displaystyle -2\]

c_0 = c_k.subs(k, 0).doit()
c_0

\[\displaystyle \frac{\pi^{2}}{3}\]

c_p1 = c_k.subs(k, 1).subs(T, 2*pi).doit()
c_p1

\[\displaystyle -2\]

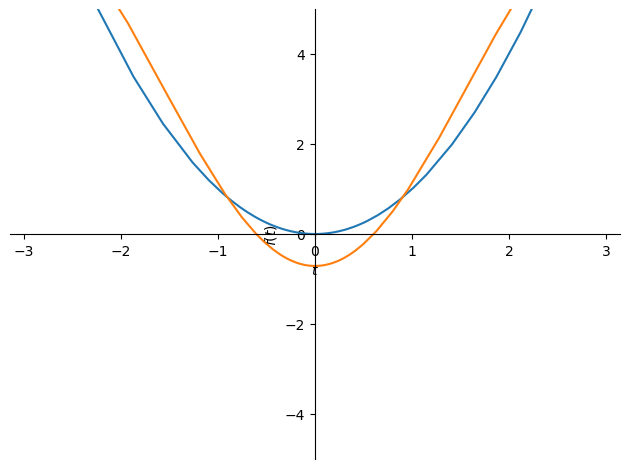
計算された複素フーリエ係数をもとに複素フーリエ級数展開する．今回は \(k=-1,0,1\) の三項のみでの近似より以下の式を定義している．

\[ f(t) = C_{-1} e^{-i \omega_0 t} + C_0 + C_1 e^{i\omega_0 t} \]

ff_approx = c_m1 * exp(k * I * omega_0 * t).subs(k, -1) + c_0 \
    + c_p1 * exp(k * I * omega_0 * t).subs(k, 1)
ff_approx

\[\displaystyle - 2 e^{i t} + \frac{\pi^{2}}{3} - 2 e^{- i t}\]

これをプロットしてみる．

plot(f, ff_approx, xlim=(-pi, pi), ylim=(-5, 5))

<sympy.plotting.plot.Plot at 0x7fa24ac0b190>

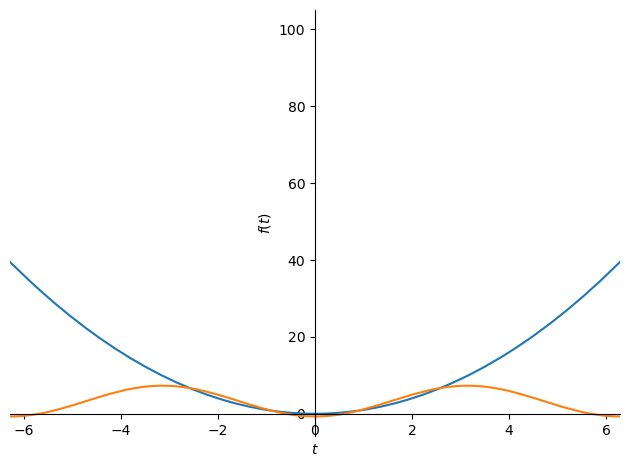
区間外もプロットしてみる．周期関数による近似のため区間外で近似が行えていないことがわかる．

plot(f, ff_approx.subs(T, 2*pi), xlim=(-2*pi, 2*pi))

<sympy.plotting.plot.Plot at 0x7fa24abc7160>

指数関数表記の三角関数の直交性

複素フーリエ級数を展開してみると

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \\ &= \cdots + C_{-k} e^{-ik\omega_0 t} + \cdots + C_0 + \cdots + C_k e^{ik\omega_0 t} + \cdots \end{align} \end{split}\]

となり，関数系が \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) であることがわかる．この関数系 \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) は 直交基底 である．

直交基底

計量空間 \(\mathcal{L}\) の任意の元の直交系 \(\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\) による最小二乗法の近似が近似対象 \(\mathbf{u}\) に一致するとき，\(\{ \mathbf{e}_i \}^n_{i=1}\) は\(\mathcal{L}\) の直交基底であるという．

では，関数系 \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) が直交する（=自身以外との内積が \(0\)）であることを確認する．区間 \([a,b]\) 上の複素数を含む関数 \(f(x),g(x)\) の内積は以下で定義される．

\[ \int_{a}^{b}\ f(x) \overline{g(x)} dx= 0 \]

ただし，\(\overline{g(x)}\) は \(g(x)\) の共役な複素数であり，実関数では \(\overline{g(x)}=g(x)\) となり，関数の内積と一致することに注意されたい．

この定義をもとに直交性を検証する．そのために，区間 \([-T/2, T/2]\) 上で二つの関数 \(e^{im\omega_0 t}, e^{in\omega_0 t}\) を関数系 \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) から取り出す．ここで \(m=n\) のとき内積の結果は以下となる．

\[\begin{split} \begin{align} \int_{-T/2}^{T/2} e^{im\omega_0 t} \overline{e^{in\omega_0 t}} dt &= \int_{-T/2}^{T/2} e^{im\omega_0 t} e^{-in\omega_0 t} dt \\ &= \int_{-T/2}^{T/2} e^{i (m-n) \omega_0 t} dt \\ &= \int_{-T/2}^{T/2} e^{0} dt \\ &= T \end{align} \end{split}\]

同様にして，\(m \neq n\) のときを検証する．

\[\begin{split} \begin{align} \int_{-T/2}^{T/2} e^{im\omega_0 t} \overline{e^{in\omega_0 t}} dt &= \int_{-T/2}^{T/2} e^{im\omega_0 t} e^{-in\omega_0 t} dt \\ &= \int_{-T/2}^{T/2} e^{i (m-n) \omega_0 t} dt \\ &= \left [ \frac{1}{i (m-n) \omega_0} e^{i (m-n) \omega_0 t} \right ]^{T/2}_{-T/2} \\ &= \frac{1}{i (m-n) \omega_0} \left \{ e^{i (m-n) \omega_0 \frac{T}{2}} - e^{- i (m-n) \omega_0 \frac{T}{2}} \right \} \\ &= \frac{1}{i (m-n) \omega_0} \left \{ e^{i (m-n) \frac{2\pi}{T}\frac{T}{2}} - e^{- i (m-n) \frac{2\pi}{T} \frac{T}{2}} \right \} \\ &= \frac{1}{i (m-n) \omega_0} \left \{ e^{i (m-n) \pi} - e^{- i (m-n) \pi} \right \} \\ &= \frac{1}{i (m-n) \omega_0} \left \{ 2i \sin \left ( m-n \right ) \pi \right \} \\ &= 0 \end{align} \end{split}\]

以上より，関数系 \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) は以下のように直交することがわかった．

\[\begin{split} \int_{-T/2}^{T/2} e^{im\omega_0 t} \overline{e^{in\omega_0 t}} dt = \begin{cases} T & m=n \\ 0 & m \neq n \end{cases} \end{split}\]

Pythonによる直交性の検証

前述の話をsympyで確認してみよう．まずは \(k=-1\) 同士の内積を計算する．

exp(k * I * omega_0 * t).subs(k, -1)

\[\displaystyle e^{- i t}\]

exp(k * I * omega_0 * t).subs(k, -1).conjugate()

\[\displaystyle e^{i \overline{t}}\]

expr = Integral(exp(k * I * omega_0 * t).subs(k, -1) * exp(k * I * omega_0 * t).subs(k, -1).conjugate(), (t, -T/2, T/2))
expr

\[\displaystyle \int\limits_{- \pi}^{\pi} e^{- i t} e^{i \overline{t}}\, dt\]

expr.doit()

\[\displaystyle 2 \pi\]

自身との内積は \(0\) とならず \(T=2\pi\) が得られ，計算結果と一致したことがわかった．続いて， \(k=1\) と \(k=-1\) の内積を計算する．

expr = Integral(exp(k * I * omega_0 * t).subs(k, 1) * exp(k * I * omega_0 * t).subs(k, -1).conjugate(), (t, -T/2, T/2))
expr

\[\displaystyle \int\limits_{- \pi}^{\pi} e^{i t} e^{i \overline{t}}\, dt\]

expr.doit()

\[\displaystyle 0\]

こちらは \(0\) となり内積が \(0\) となることを確認できた．

直交性からの複素フーリエ級数と係数の導出

直交であることがわかったので，実関数のフーリエ級数展開と同様に，直交性から複素フーリエ係数を導出することを試みる．そのために関数 \(f(t)\) を区間 \([-T/2,T/2]\) 上で関数系 \(\{e^{ik\omega_0 t}|k\in\mathbb{Z}\}\) の線形結合で近似することを考える．

\[\begin{split} \begin{align} f(t) &= \sum_{k=-\infty}^{\infty} C_k e^{ik \omega_0 t} \\ &= \cdots + C_{-k} e^{-ik\omega_0 t} + \cdots + C_0 + \cdots + C_k e^{ik\omega_0 t} + \cdots \end{align} \end{split}\]

両辺に \(e^{-ik \omega_0 t}\) をかけて区間 \([-T/2,T/2]\) 上で積分する．

\[\begin{split} \begin{align} \int_{-T/2}^{T/2} f(t) e^{-ik\omega_0 t} dt &= \cdots + C_{-k} \int_{-T/2}^{T/2} e^{-ik\omega_0 t} e^{-ik\omega_0 t} dt + \cdots \\ & \quad + C_0 \int_{-T/2}^{T/2} e^{-ik\omega_0 t} dt + \cdots \\ & \quad + C_k \int_{-T/2}^{T/2} e^{ik\omega_0 t} e^{-ik\omega_0 t} dt + \cdots \end{align} \end{split}\]

直交性の定義より，\(C_k\) 以外はすべて \(0\) となるので以下のように複素フーリエ係数が導出できる．

\[\begin{split} \begin{align} \int_{-T/2}^{T/2} f(t) e^{-ik\omega_0 t} dt &= C_k \int_{-T/2}^{T/2} e^{ik\omega_0 t} e^{-ik\omega_0 t} dt \\ &= C_k T \\ C_k &= \frac{1}{T} \int_{-T/2}^{T/2} f(t) e^{-ik\omega_0 t} dt \end{align} \end{split}\]

以上より，直交性より複素フーリエ級数と係数を導出できた．