角周波数でのフーリエ級数展開

角周波数へのフーリエ級数展開の拡張

フーリエ級数展開によって与えられた関数を異なる周期を持つ三角関数の線形結合で表現できた．ここで複素フーリエ級数展開とフーリエ変換のための単位時間における回転角の変化量でフーリエ級数展開を書き換える．この目的としては，角度 \(\theta(=x)\) のフーリエ級数展開から時間 \(t\) のフーリエ級数展開へ解釈することにある．

復習となるが，フーリエ級数展開のベースとなっている三角関数は一定間隔（周期 \(T>0\)）で同じ値を繰り返す周期関数であった．

\[ f(x+T)=f(x) \]

そして，\(\cos kx\) の周期を例にすると，その周期は \(\cos x\) のグラフを \(x\) 軸方向に \(1/k\) 倍したものであった．これは言い換えると周期は \(2 \pi / k\)である．これを sympy を使って確認する．

from sympy import symbols, sin, cos, pi
from sympy.plotting import plot

x = symbols('x')

f_cosx = cos(x)
f_cos2x = cos(2*x)
f_cos3x = cos(3*x)
f_cos4x = cos(4*x)
plot(f_cosx, f_cos2x, f_cos3x, f_cos4x, (x, -pi, pi))

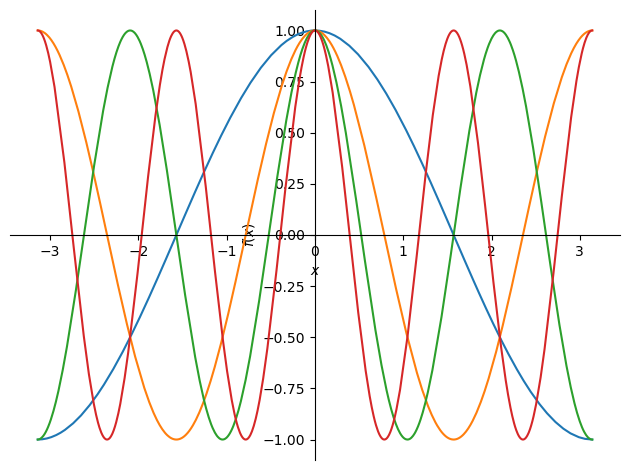
<sympy.plotting.plot.Plot at 0x7f82b361caf0>

ここで，波のパターンの時間である周期ではなく，ある単位時間に含まれる波形の数を考える．これは 周波数 と呼ばれ，周波数 \(v\) は周期 \(T\) と次のような関係性を持つ．

\[ v = \frac{1}{T} \]

そして，\(\sin\)関数と\(\cos\)関数の正弦波が角度 \(\theta(=x)\) に関する関数であったが，単位時間の回転角の変化量 \(\omega\) と時刻 \(t\) の関数として解釈する．ここで，時刻 \(t\) の回転角 \(\theta\) は単位時間の回転角の変化量 \(\omega\) を使って以下のように書ける．

\[ \theta = \omega t \]

このとき円の一周分は \(2 \pi\) より周波数を角周波数で書くと

\[ v = \frac{\omega}{2 \pi} \]

となる．\(v = 1/T\) であったので角周波数と周期の関係は以下のようになる．

\[ \omega = \frac{2 \pi}{T} \]

以上より，角度 \(\theta(=x)\) から時間 \(t\) の関数としてフーリエ級数展開を解釈する準備ができた．

補足となるが角度 \(\theta(=x)\) から時間 \(t\) の関数を図でプロットすると以下のようになる．

import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))
theta = np.linspace(0, 2*np.pi, 360)
x = np.cos(theta)
y = np.sin(theta)

deg = 45
px = np.cos(np.deg2rad(deg))
py = np.sin(np.deg2rad(deg))

pad = 0.05
ax.scatter(px, py, c="r")
ax.text(px+pad, py+pad, "P", color="r", fontsize=16)

ax.scatter(px, 0, c="b")
ax.text(px+pad, pad, "cosθ", color="b", fontsize=16)

ax.scatter(0, py, c="b")
ax.text(pad, py+pad, "sinθ", color="b", fontsize=16)

ax.plot([-1,1],[0,0], color="k", linewidth=1)
ax.plot([0,0],[-1,1], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([0,px],[0,py], color="k", linewidth=1)
ax.plot([px,px],[0,py], color="k", linewidth=1, linestyle="--")
ax.plot([0,px],[py,py], color="k", linewidth=1, linestyle="--")

ax.text(pad+0.1, pad, "θ=ωt", color="b", fontsize=16)

ax.grid()
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(-1.1, 1.1)
ax.plot(x, y, color='k')

[<matplotlib.lines.Line2D at 0x7f82b45fdb20>]

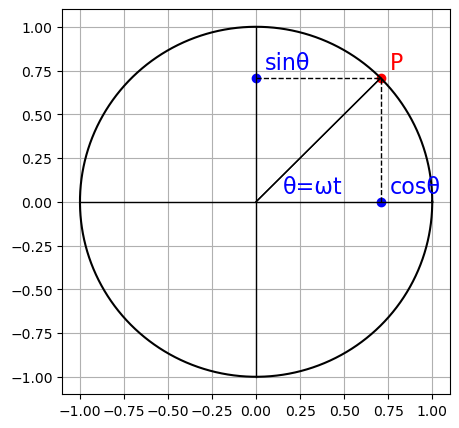
では，ここから角度 \(\theta(=x)\) から時間 \(t\) の関数としてフーリエ級数展開を置き換える．具体的に，基本周波数 \(\omega_0 = \frac{2\pi}{T}\) の関数としての正弦波

\[\begin{split} \begin{align} f(t) = \cos \omega_0 t \\ f(t) = \sin \omega_0 t \end{align} \end{split}\]

でフーリエ級数を表現する．上記で導出した関係式より，

\[ \begin{align} \theta = x = \omega t = \frac{2\pi t}{T} \end{align} \]

であることがわかっている．また直交性を検証した区間は以下のように周期 \(T\) を使って書ける．

\[ -\pi \leq x \leq \pi \rightarrow -T/2 \leq t \leq T/2 \]

最後に，フーリエ係数に含まれる積分係数 \(dx\) も \(dt\) に置き換える必要がある．前述の関係式から積分範囲は以下のように変数変換される．

\[\begin{split} \begin{align} \frac{dx}{dt} &= \frac{2\pi}{T} \\ dx &= \frac{2\pi}{T} dt \end{align} \end{split}\]

以上の変更点に注意してフーリエ級数展開を書き換えると，区間 \(-T/2 \leq t \leq T/2\) 上の関数 \(f(t)\) のフーリエ級数展開を基本周波数 \(\omega_0\) の整数倍の周波数の正弦波の重ね合わせで表現することになる．そして，フーリエ級数とフーリエ係数は以下となる．

\[ \begin{align} f(t) &\approx \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \cos k \omega_0 t + b_k \sin k \omega_0 t), \quad -\frac{T}{2} \leq t \leq \frac{T}{2} \end{align} \]

\[ a_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt, \quad b_k = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \]

\(a_0\) に関しては　\(k=0\) を \(a_k\) に代入すると得られる．

\[\begin{split} \begin{align} a_0 &= \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos 0 \omega_0 t dt \\ &= \frac{2}{T} \int_{-T/2}^{T/2} f(t) dt \end{align} \end{split}\]

以上の置き換えにより，角度 \(\theta(=x)\) から時間 \(t\) の関数としてフーリエ級数展開を導出することができた．

具体例

では，区間 \([-\pi, \pi]\) 上の以下の関数 \(f(t)\) についてフーリエ級数展開してみよう．

\[\begin{split} f(t) = \begin{cases} 1 & -\pi < t \leq 0 \\ 0 & 0 < t \leq \pi \end{cases} \end{split}\]

解答はクリックで確認できる．

フーリエ係数 \(a_0, a_k, b_k\) を順に計算する．まず \(\omega_0 = 2 \pi / T\) で周期 \(T = 2\pi\) より基本周波数は \(\omega_0 = 1\) であることがわかる．これよりフーリエ係数 \(a_0\) を上記で導出したフーリエ係数の式から計算する．

\[\begin{split} \begin{align} a_0 &= \frac{2}{T} \int_{-T/2}^{T/2} f(t) dt \\ &= \frac{2}{2 \pi} \int_{-\pi}^{\pi} f(t) dt \\ &= \frac{1}{\pi} \left\{ \int_{-\pi}^{0} 1 dt + \int_{0}^{\pi} 0 dt \right\} \\ &= \frac{1}{\pi} \left [ t \right ]^{0}_{-\pi} \\ &= \frac{1}{\pi} \left \{ 0 + \pi \right \} = 1 \end{align} \end{split}\]

続いて，フーリエ係数 \(a_k\) は以下のように計算できる．

\[\begin{split} \begin{align} a_k &= \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos k \omega_0 t dt \\ &= \frac{2}{2 \pi} \int_{-\pi}^{\pi} f(t) \cos kt dt \\ &= \frac{1}{\pi} \left\{ \int_{-\pi}^{0} 1 \cdot \cos kt dt + \int_{0}^{\pi} 0 \cdot \cos kt dt \right\} \\ &= \frac{1}{\pi} \left [ \frac{1}{k} \sin kt \right ]^{0}_{\pi} \\ &= \frac{1}{\pi} \left \{ \frac{1}{k} \sin 0 - \frac{1}{k} \sin \left ( -k \pi \right ) \right \} \\ &= \frac{1}{k\pi} \sin k\pi = 0 \end{align} \end{split}\]

最後に，フーリエ係数 \(b_k\) は以下のように計算できる．

\[\begin{split} \begin{align} b_k &= \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin k \omega_0 t dt \\ &= \frac{2}{2 \pi} \int_{-\pi}^{\pi} f(t) \sin kt dt \\ &= \frac{1}{\pi} \left\{ \int_{-\pi}^{0} 1 \cdot \sin kt dt + \int_{0}^{\pi} 0 \cdot \sin kt dt \right\} \\ &= \frac{1}{\pi} \left [ - \frac{1}{k} \cos kt \right ]^{0}_{\pi} \\ &= \frac{1}{\pi} \left \{ - \frac{1}{k} \cos 0 + \frac{1}{k} \cos \left ( -k \pi \right ) \right \} \\ &= - \frac{1}{k \pi} \left (1 - \cos k \pi \right ) \\ &= - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \\ \end{align} \end{split}\]

以上より，フーリエ係数が以下のように計算された．

\[ \begin{align} a_0 = 1, \quad a_k = 0, \quad b_k = - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \end{align} \]

これをフーリエ級数展開の式に代入する．

\[\begin{split} \begin{align} f(t) &\approx \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \cos k \omega_0 t + b_k \sin k \omega_0 t) = \frac{a_{0}}{2} + \sum_{k=1}^{\infty} (a_k \cos kt + b_k \sin kt) \\ &= \frac{1}{2} + \sum_{k=1}^{\infty} \left [0 \cdot \cos kt - \frac{1}{k \pi} \left \{1 - \left ( -1 \right )^k \right \} \sin kt \right] \\ &= \frac{1}{2} - \frac{1}{\pi} \sum_{k=1}^{\infty} \left [ \frac{\left \{1 - \left ( -1 \right )^k \right \}}{k} \sin kt \right] \\ &= \frac{1}{2} - \frac{2}{\pi} \sum_{n=1}^{\infty} \left [ \frac{1}{2n - 1} \sin (2n-1)t \right] \\ &= \frac{1}{2} - \frac{2}{\pi} \left ( \sin t + \frac{1}{3} \sin 3t + \frac{1}{5} \sin 5t + \cdots \right ) \end{align} \end{split}\]

以上より，与えられた関数 \(f(t)\) のフーリエ級数展開を求めることができた．

Pythonによるフーリエ級数展開の実装

では，本日説明したフーリエ級数展開をPythonで実装する．まずは時刻 \(t\) の関数 \(f(t)\) を定義する．

from sympy import symbols, cos, sin, pi
t = symbols('t')

f = 1 + 0.25 * cos(t) -1.1 * sin(2*t) + cos(3*t) - 0.4 * sin(4*t)
f

\[\displaystyle - 1.1 \sin{\left(2 t \right)} - 0.4 \sin{\left(4 t \right)} + 0.25 \cos{\left(t \right)} + \cos{\left(3 t \right)} + 1\]

from sympy.plotting import plot
plot(f, xlim=(-pi, pi) , ylim=(-5, 5))

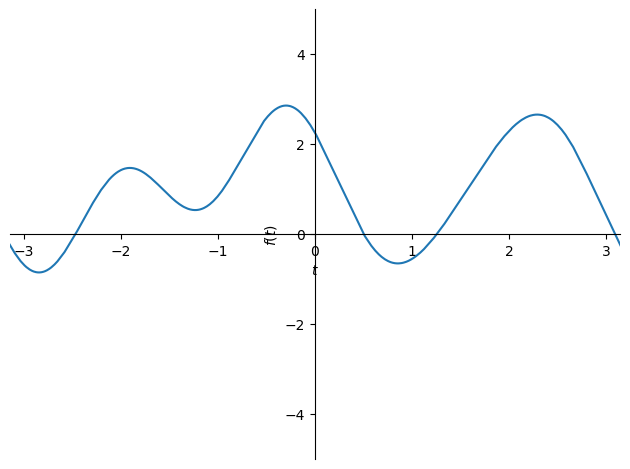
<sympy.plotting.plot.Plot at 0x7f82b473bdf0>

続いて，基本周波数 \(\omega_0 = 2\pi / T\) を定義する．

T = symbols('T', real=True)
omega_0 = 2 * pi / T
omega_0

\[\displaystyle \frac{2 \pi}{T}\]

そして，導出したフーリエ係数 \(a_k, b_k\) の式に基づいてこれらを実装する．

from sympy import Integral
k = symbols('k')
a_k = Integral(f * cos(k * omega_0 * t), (t, -T/2, T/2)) * 2 / T
a_k

\[\displaystyle \frac{2 \int\limits_{- \frac{T}{2}}^{\frac{T}{2}} \left(- 1.1 \sin{\left(2 t \right)} - 0.4 \sin{\left(4 t \right)} + 0.25 \cos{\left(t \right)} + \cos{\left(3 t \right)} + 1\right) \cos{\left(\frac{2 \pi k t}{T} \right)}\, dt}{T}\]

b_k = Integral(f * sin(k * omega_0 * t), (t, -T/2, T/2)) * 2 / T
b_k

\[\displaystyle \frac{2 \int\limits_{- \frac{T}{2}}^{\frac{T}{2}} \left(- 1.1 \sin{\left(2 t \right)} - 0.4 \sin{\left(4 t \right)} + 0.25 \cos{\left(t \right)} + \cos{\left(3 t \right)} + 1\right) \sin{\left(\frac{2 \pi k t}{T} \right)}\, dt}{T}\]

定義できたので，フーリエ係数の計算を実行する．今回は\(k=3\)まで展開してみよう．具体的には\(k\)番目の項と周期\(T\)を変数として定義していたのでsubs()で代入し，上記で定義した\(a_k,b_k\)の積分を.doit()で実行できる．

a_0 = a_k.subs(k, 0).subs(T, 2*pi).doit()
a_0

\[\displaystyle 2\]

a_1 = a_k.subs(k, 1).subs(T, 2*pi).doit()
a_1

\[\displaystyle 0.25\]

a_2 = a_k.subs(k, 2).subs(T, 2*pi).doit()
a_2

\[\displaystyle 0\]

a_3 = a_k.subs(k, 3).subs(T, 2*pi).doit()
a_3

\[\displaystyle 1.0\]

b_0 = b_k.subs(k, 0).subs(T, 2*pi).doit()
b_0

\[\displaystyle 0\]

b_1 = b_k.subs(k, 1).subs(T, 2*pi).doit()
b_1

\[\displaystyle 0\]

b_2 = b_k.subs(k, 2).subs(T, 2*pi).doit()
b_2

\[\displaystyle -1.1\]

b_3 = b_k.subs(k, 3).subs(T, 2*pi).doit()
b_3

\[\displaystyle 0\]

計算された \(k=3\) までのフーリエ係数をもとにフーリエ級数展開する．

ff_approx = a_0 / 2 + a_1 * cos(omega_0*t) + b_1 * sin(omega_0*t) \
    + a_2 * cos(2*omega_0*t) + b_2 * sin(2*omega_0*t) \
    + a_3 * cos(3*omega_0*t) + b_3 * sin(3*omega_0*t)

omega_0は変数Tを含むのでsubs()で代入する．

ff_approx.subs(T, 2*pi)

\[\displaystyle - 1.1 \sin{\left(2 t \right)} + 0.25 \cos{\left(t \right)} + 1.0 \cos{\left(3 t \right)} + 1\]

近似対象と比較をするために同時にプロットしてみる．

plot(f, ff_approx.subs(T, 2*pi), xlim=(-pi, pi))

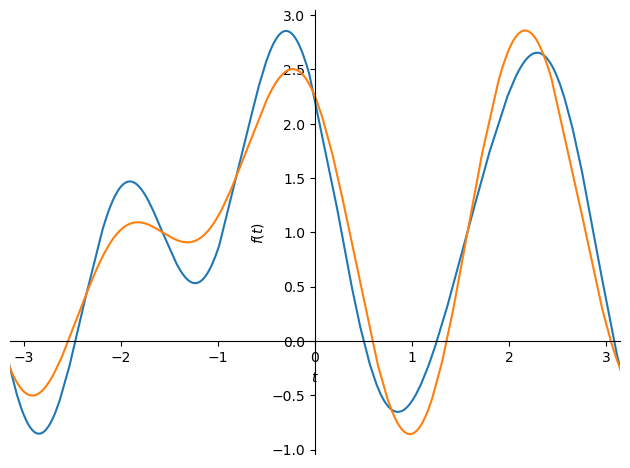
<sympy.plotting.plot.Plot at 0x7f82b4999d30>

区間外もプロットしてみる．

plot(f, ff_approx.subs(T, 2*pi), xlim=(-2*pi, 2*pi))

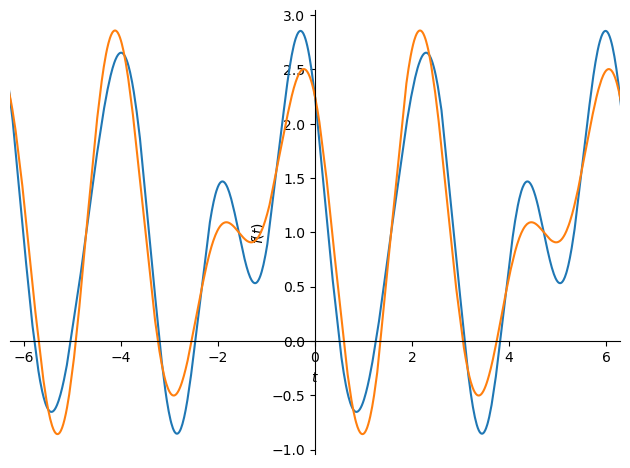
<sympy.plotting.plot.Plot at 0x7f82702de820>