最小二乗法
関数の足し合わせによる関数の近似を理解するために 最小二乗法 を紹介する.最小二乗法では,データを与えられそのデータをよく表現する関数を求める 関数近似 を行う.関数近似によってデータの背後に潜む関係性を関数として捉えることができれば,データ間の対応関係や未知のデータに対する予測が可能となる.
例えば,以下のように何らかのデータを取得したとしよう.プログラムとしては,\(y=2x+1\)の関係が背後に潜むノイズの乗ったデータを擬似的に生成している.matplotlibを使って生成したデータ(青色の点)とその背後に潜む関係性(赤色の直線)をプロットしている.
[<matplotlib.lines.Line2D at 0x7f7d1c2b4fd0>]
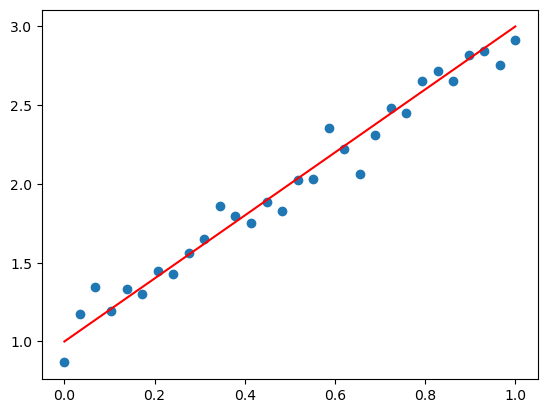
関数近似の目的は,\(x\) を入力値,\(y\) を \(x\) に対応する目標値としたとき,\(N\) 個のデータ \(\{(x_i,y_i)\}_{i=1}^N\) からデータの背後に潜む赤色の関係性を求めることである.しかしながら,利用できるデータはここでは x_data と y_data のみであり,関係性に関する情報(関数の形など)は未知である.
そこで最小二乗法では,\(N\) 個のデータ \(\{(x_i,y_i)\}_{i=1}^N\) を与えられ,\(n\)個のの関数の値 \(\phi_{k}(x)\) とその係数 \(c_k\) との定数倍の和で表現される関数を考える(\(k=1,...,n\))
\[
y_{\alpha} \approx \sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right), \alpha=1, \ldots, N
\]
この関数が成立するような係数 \(c_1,...,c_n\) を求めることがゴールであり,これらの係数は以下の最小化問題から求めることができる.
\[
J=\frac{1}{2} \sum_{\alpha=1}^{N}\left(y_{\alpha}-\sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right)\right)^{2} \rightarrow \min
\]
線型結合
前述の定数倍の和で表される第一式は係数 \(c\) と関数 \(\phi\) の値の足し合わせ(線型結合)になっていることが以下のように展開するとわかる.
\[\begin{split}
\begin{align}
y_{\alpha} &\approx \sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right) \\
&=c_{1} \phi_{1}\left(x_{\alpha}\right) + c_{2} \phi_{2}\left(x_{\alpha}\right) + \cdots
\end{align}
\end{split}\]
上記の例のように直線で近似することを考えると,\(\{\phi_1, \phi_2, c_1, c_2\}=\{1,x,b,a\}\) とすれば,上記の式は,\(y_{\alpha} \approx ax_{\alpha}+b\) となり,直線の方程式 \(y=ax+b\) の係数 \(a,b\) をデータから求める問題になっていることがわかる.さらに,\(\{\phi_1, \phi_2, \phi_3, c_1, c_2, c_3\}=\{1,x,x^2, c, b,a\}\) とすれば,二次関数 \(y_{\alpha} \approx ax_{\alpha}^{2}+bx_{\alpha} + c\) で関数を近似することとなる.
ここまで考えると,\(\{\phi_1, \phi_2, \phi_3\}=\{1,\cos{x},\sin{x}\}, \{c_1, c_2, c_3\}=\{a_0, a_1, b_1\}\) とすれば,\(y_{\alpha} \approx a_0 + a_1 \cos{x_{\alpha}} + b_1 \sin{x_{\alpha}}\) となり,最小二乗法からフーリエ級数展開の式が書けそうなのがイメージできるかと思う.
では,係数 \(c_k\) を求める最小化問題を深掘りする.二つ目のシグマを展開してみると,
\[
\begin{align}
J&=\frac{1}{2} \sum_{\alpha=1}^{N}\left(y_{\alpha}-\left ( c_{1} \phi_{1}\left(x_{\alpha}\right) + c_{2} \phi_{2}\left(x_{\alpha}\right) + \cdots \right )\right)^{2}
\end{align}
\]
となり,係数 \(c\) をもつ関数 \(\phi\) の線形結合の式と \(y_{\alpha}\) との差の計算をしていることがわかる.そして残ったシグマも展開してみると,
\[\begin{split}
\begin{align}
J= &\frac{1}{2} \left ( \left(y_{1}-\left ( c_{1} \phi_{1}\left(x_{1}\right) + c_{2} \phi_{2}\left(x_{1}\right) + \cdots \right )\right)^{2} \right. \\
& \left. + \left(y_{2}-\left ( c_{1} \phi_{1}\left(x_{2}\right) + c_{2} \phi_{2}\left(x_{2}\right) + \cdots \right )\right)^{2} + \cdots \right )
\end{align}
\end{split}\]
となり,すべてのデータの差を足していることがわかる.つまりはデータを表現する関数 \(\phi\) は固定で \(c\) の値を変化させて関数と実際に観測されたデータの値との差(=\(J\))をできるだけ小さくする問題を考えているのである.そして,\(J\)を小さくする\(c\)を求める方法はこれまで最小値の問題を解いてきた時と同じように関数の傾きを考え,傾きが\(0\)となる点を求めれば良い.ただし,今回は \(J\) は多変数関数なので偏微分を考える必要がある.
\(J\) を \(c_i\) で偏微分したときの偏導関数を求める(慣れるまではシグマを展開して偏微分すると良い).
\[
\frac{\partial J}{\partial c_i}= \sum_{\alpha=1}^{N}\left(y_{\alpha}-\sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right)\right)\left ( - \phi_{i} \left(x_{\alpha}\right) \right )
\]
そして,全ての係数 \(c_1,...,c_n\) の偏導関数について以下の方程式を解く.
\[
\frac{\partial J}{\partial c_1}=0, \cdots, \frac{\partial J}{\partial c_n}=0
\]
この連立方程式を解くために 正規方程式 と呼ばれる行列で表現される形に書き換える.まず求めたい \(c\) について偏導関数を整理する.
\[\begin{split}
\begin{align}
\frac{\partial J}{\partial c_i} &= \sum_{\alpha=1}^{N}\left(y_{\alpha}-\sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right)\right)\left ( - \phi_{i} \left(x_{\alpha}\right) \right ) \\
&=- \sum_{\alpha=1}^{N} y_{\alpha} \phi_{i} \left(x_{\alpha}\right) + \sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{i} \left(x_{\alpha}\right) \right ) c_{k}
\end{align}
\end{split}\]
ここで,\( \partial J / \partial c_i = 0 \) より,
\[
\sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{i} \left(x_{\alpha}\right) \right ) c_{k} = \sum_{\alpha=1}^{N} y_{\alpha} \phi_{i} \left(x_{\alpha}\right)
\]
となる.これをすべての係数で並べてみると,
\[\begin{split}
\left\{\begin{matrix}
\sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{1} \left(x_{\alpha}\right) \right ) c_{k} = \sum_{\alpha=1}^{N} y_{\alpha} \phi_{1} \left(x_{\alpha}\right)\\
\sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{2} \left(x_{\alpha}\right) \right ) c_{k} = \sum_{\alpha=1}^{N} y_{\alpha} \phi_{2} \left(x_{\alpha}\right)\\
\vdots \\
\sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{n} \left(x_{\alpha}\right) \right ) c_{k} = \sum_{\alpha=1}^{N} y_{\alpha} \phi_{n} \left(x_{\alpha}\right)\\
\end{matrix}\right.
\end{split}\]
となり,以下のように行列の形で書き直すことができる.
\[\begin{split}
\begin{pmatrix}
\sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) \phi_{1}\left(x_{\alpha}\right) & \sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) \phi_{2}\left(x_{\alpha}\right) & \cdots & \sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) \phi_{n}\left(x_{\alpha}\right) \\
\sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) \phi_{1}\left(x_{\alpha}\right) & \sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) \phi_{2}\left(x_{\alpha}\right) & \cdots & \sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) \phi_{n}\left(x_{\alpha}\right) \\
\vdots & \vdots & \ddots & \vdots \\
\sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) \phi_{1}\left(x_{\alpha}\right) & \sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) \phi_{2}\left(x_{\alpha}\right) & \cdots & \sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) \phi_{n}\left(x_{\alpha}\right)
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) y_{\alpha} \\
\sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) y_{\alpha} \\
\vdots \\
\sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) y_{\alpha}
\end{pmatrix}
\end{split}\]
この方程式を解けば係数 \(c\) を求めることができ,最小二乗法による関数近似を実現できる.
行列への変換
2つ以上のシグマを含む偏導関数を行列の形式へ変換するのはやや慣れが必要かもしれない.初めのうちは以下のようにシグマを展開して考えてみると良い(\(c_1\)の偏導関数の展開).
\[ \begin{align}\begin{aligned}c_{1} \sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) \phi_{1} \left(x_{\alpha}\right) +
c_{2} \sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) \phi_{1} \left(x_{\alpha}\right) +
\cdots +
c_{n} \sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) \phi_{1} \left(x_{\alpha}\right)\\= \sum_{\alpha=1}^{N} y_{\alpha} \phi_{1} \left(x_{\alpha}\right)\end{aligned}\end{align} \]
正規方程式の行列計算で偏導関数が表現できていることが確認できると思う.
Pythonによる実装
では,先ほど作成した x_data と y_data から最小二乗法を実装してみる.今回は以下の線型結合で表される式,
\[
y_{\alpha} \approx \sum_{k=1}^{n} c_{k} \phi_{k}\left(x_{\alpha}\right), \alpha=1, \ldots, N
\]
について,前述したように,\(\{\phi_1, \phi_2, c_1, c_2\}=\{1,x,b,a\}\) として一次関数
\[y_{\alpha} \approx ax_{\alpha}+b\]
を考える.このとき \(N\) はデータ数.つまり x_data.shape[0]としたときの値である.まずは \(N\) を確認する.
x_data を作成したときの N と一致していることを確認されたい.続いて,式をsympyで定義していく.
\[\displaystyle a x + b\]
続いて,\(J\) を定義する.numpy表記のように書けるのでプログラムは簡単に書ける
\[\displaystyle \frac{\left(- a x - b + y\right)^{2}}{2}\]
今回,係数は \(a\)と\(b\)である.これらのパラメータに対する偏導関数\(\frac{\partial J}{\partial a}, \frac{\partial J}{\partial b}\)を定義する.
\[\displaystyle - x \left(- a x - b + y\right)\]
\[\displaystyle a x + b - y\]
得られた偏導関数について,各データを代入して方程式を得る.具体的には次の式の計算を各係数\(a,b\)について行っている.
\[
\sum_{\alpha=1}^{N} y_{\alpha} \phi_{i} \left(x_{\alpha}\right) + \sum_{k=1}^{n} \left ( \sum_{\alpha=1}^{N} \phi_{k}\left(x_{\alpha}\right) \phi_{i} \left(x_{\alpha}\right) \right ) c_{k}
\]
\[\displaystyle 10.1724137931034 a + 15.0 b - 34.9524330405871\]
\[\displaystyle 15.0 a + 30 b - 59.7269328906071\]
得られた連立方程式を solve を使って解いて係数\(a,b\)を求める.行っている計算は正規方程式を解いているのと同じである.
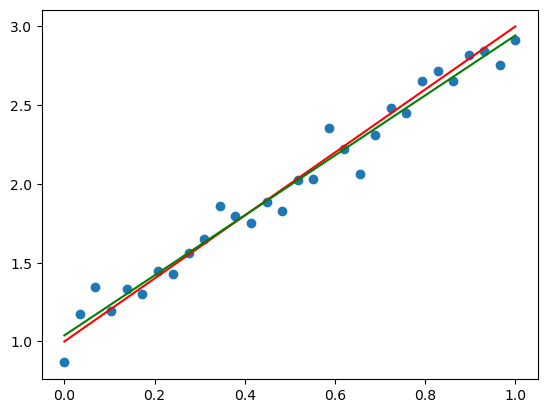
{a: 1.90425846791255, b: 1.03876852906396}
得られた係数\(a,b\)が実際の値に近いことがわかる.実際にプロットもしてみる
[<matplotlib.lines.Line2D at 0x7f7d1c3e1880>]
直交関数系
正規方程式からパラメータ \(c_k\) を求めることができたが,関数 \(\phi\) を自身以外との積が \(0\) となるように関数の集合 \(\{ \phi_{i}(x) \}^{n}_{i=1}\) を設計するとさらに計算が簡単になる.この自身以外との積が \(0\) となるような性質を 直交性 と言い,以下で定義される.
\[
\sum_{\alpha=1}^{N} \phi_{i}\left(x_{\alpha}\right) \phi_{j}\left(x_{\alpha}\right) = 0, \qquad i \neq j
\]
そして,直交性を持つ関数の集合を 直交関数系 と言う.
直交関数系で関数 \(\phi\) を設計したときの正規方程式を考えると,自身以外との積が \(0\) となるので正規方程式の非対角成分が \(0\) となるのは明らかである.
\[\begin{split}
\begin{pmatrix}
\sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) \phi_{1}\left(x_{\alpha}\right) & & & \\
& \sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) \phi_{2}\left(x_{\alpha}\right) & & \\
& & \ddots & \\
& & & \sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) \phi_{n}\left(x_{\alpha}\right)
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\sum_{\alpha=1}^{N} \phi_{1}\left(x_{\alpha}\right) y_{\alpha} \\
\sum_{\alpha=1}^{N} \phi_{2}\left(x_{\alpha}\right) y_{\alpha} \\
\vdots \\
\sum_{\alpha=1}^{N} \phi_{n}\left(x_{\alpha}\right) y_{\alpha}
\end{pmatrix}
\end{split}\]
つまりは各成分 \(c_i\) は以下の式から容易に計算できる.
\[
c_i = \frac{\sum_{\alpha=1}^{N} \phi_{i} \left(x_{\alpha}\right) y_{\alpha}}{\sum_{\alpha=1}^{N} \phi_{i}\left(x_{\alpha}\right)^2 }, \qquad i=1,...,n
\]
ベクトルの直交
正規方程式は自身以外との積が \(0\) となるように関数を設計することで簡単に解くことができたが,近似対象が\(N\) 個の離散データ \(\{(x_i,y_i)\}_{i=1}^N\) ではなくベクトルや関数そのものであったときどのように最小二乗法や直交性を考えるべきかをここで紹介する.
そもそも 直交する という表現はこれまでベクトルで登場したかと思う.具体的には,\(m\)次元のベクトル \(\mathbf{a}, \mathbf{b}\) の内積が \(0\) であるときこれらのベクトルは直交していると習ったはずだ.
\[
\left (\mathbf{a}, \mathbf{b} \right ) = \sum_{i=1}^m a_i b_i = a_1 b_1 + \cdots + a_m b_m = 0
\]
そして,ベクトルが直交するとは二つのベクトルが成す角が\(90°\)であった.このベクトルの直交性は,ベクトルを最小二乗法で近似する場合に直接利用することもできる.
以下にベクトルの最小二乗法についてまとめた.クリックすると確認できる.
ベクトルの最小二乗法と直交性
先ほどの離散データにおける最小二乗法と同様に,\(m\) 次元列ベクトル \(\mathbf{a}\) を \(n\) 本の任意の\(m\) 次元ベクトル \(\{ \mathbf{u}_i \}^n_{i=1}\) の線形結合で表現する最小二乗法を考える.このときのベクトルの線型結合は
\[\begin{split}
\begin{align}
\mathbf{a} &\approx \sum_{k=1}^{n} c_{k} \mathbf{u}_k \\
&=c_1 \mathbf{u}_1 + c_2 \mathbf{u}_2 + \cdots c_n \mathbf{u}_n
\end{align}
\end{split}\]
として表され,最小二乗法としてすべての成分を均一に近似するように最小化問題を考えることができる.
\[
J = \frac{1}{2} \left \| \mathbf{a} - \sum^{n}_{k=1} c_k \mathbf{u}_k \right \|^2 \rightarrow min
\]
同じく,関数 \(J\) についてその偏導関数が \(0\) となるように係数 \(\{ c_i \}^n_{i=1}\) を求める.偏導関数は以下であり,
\[
\frac{\partial J}{\partial c_i} = -\left ( \mathbf{a}, \mathbf{u}_i \right ) + \sum_{k=1}^{n} c_k \left (\mathbf{u}_k, \mathbf{u}_i \right )
\]
正規方程式は以下となる.
\[\begin{split}
\begin{pmatrix}
\left \| \mathbf{u}_1\right \| &
\left ( \mathbf{u}_1, \mathbf{u}_2 \right ) &
\cdots &
\left ( \mathbf{u}_1, \mathbf{u}_n \right ) \\
\left ( \mathbf{u}_2, \mathbf{u}_1 \right ) &
\left \| \mathbf{u}_2 \right \| &
\cdots &
\left ( \mathbf{u}_2, \mathbf{u}_n \right ) \\
\vdots & \vdots & \ddots & \vdots \\
\left ( \mathbf{u}_n, \mathbf{u}_1 \right ) &
\left ( \mathbf{u}_n, \mathbf{u}_2 \right ) &
\cdots &
\left \| \mathbf{u}_n \right \|
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\left ( \mathbf{a}, \mathbf{u}_1 \right ) \\
\left ( \mathbf{a}, \mathbf{u}_2 \right ) \\
\vdots \\
\left ( \mathbf{a}, \mathbf{u}_n \right )
\end{pmatrix}
\end{split}\]
ここでも自身との内積が \(0\) となるような列ベクトルの集合 \(\{ \mathbf{u}_i \}^n_{i=1}\) であると,以下のように正規方程式の非対角成分は \(0\) となり,
\[\begin{split}
\begin{pmatrix}
\left \| \mathbf{u}_1\right \| &
&
&
\\
&
\left \| \mathbf{u}_2 \right \| &
&
\\
&& \ddots & \\
&
&
&
\left \| \mathbf{u}_n \right \|
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\left ( \mathbf{a}, \mathbf{u}_1 \right ) \\
\left ( \mathbf{a}, \mathbf{u}_2 \right ) \\
\vdots \\
\left ( \mathbf{a}, \mathbf{u}_n \right )
\end{pmatrix}
\end{split}\]
各係数 \(c_i\) は簡単に計算できる.
\[
c_i = \frac{\left (\mathbf{a}, \mathbf{u}_i \right )}{\left \| \mathbf{u}_i \right \|^ 2}, \qquad i=1,\ldots n
\]
ここからさらに,\(\mathbf{u}\) を直交かつ単位ベクトルとなるように設計することを考える.
\[
\left \| \mathbf{u}_i \right \| = 1, \qquad i=1,\ldots,n
\]
このように \(\{ \mathbf{u}_i \}^n_{i=1}\) のすべての要素が単位ベクトルであるとき 正規直交系 と呼び,\(c_i\)の解はさらにシンプルになる.
\[
c_i = \left (\mathbf{a}, \mathbf{u}_i \right ), \qquad i=1,\ldots n
\]
ベクトルのノルム
ベクトルのノルムは内積を用いて以下で定義される.
\[
\left \| \mathbf{a} \right \| = \sqrt{\left ( \mathbf{a}, \mathbf{a} \right )} = \sqrt{\sum^{m}_{i=1} a_i^2}
\]
偏導関数の導出
\(\partial J / \partial c_i\)の式変形についてまとめたので参考にされたい.
\[\begin{split}
\begin{align}
\frac{\partial J}{\partial c_i} &= \frac{\partial}{\partial c_i} \left \{ \frac{1}{2} \left \| \mathbf{a} - \sum^{n}_{k=1} c_k \mathbf{u}_k \right \|^2 \right \} \\
&=\frac{\partial}{\partial c_i} \left \{ \frac{1}{2} \left ( \mathbf{a} - \sum^{n}_{k=1} c_k \mathbf{u}_k, \mathbf{a} - \sum^{n}_{l=1} c_l \mathbf{u}_l \right ) \right \} \\
&=\frac{\partial}{\partial c_i} \left \{ \frac{1}{2} \left ( \left ( \mathbf{a}, \mathbf{a} \right ) - 2 \left ( \mathbf{a}, \sum^{n}_{k=1} c_k \mathbf{u}_k \right ) + \left ( \sum^{n}_{k=1} c_k \mathbf{u}_k, \sum^{n}_{l=1} c_l \mathbf{u}_l \right )\right ) \right \} \\
&=\frac{\partial}{\partial c_i} \left \{ \frac{1}{2} \left (\left \| \mathbf{a} \right \| ^2 - 2 \sum^{n}_{k=1} c_k \left ( \mathbf{a}, \mathbf{u}_k \right ) + \sum^{n}_{k=1} \sum^{n}_{l=1} c_k c_l \left ( \mathbf{u}_k, \mathbf{u}_l \right )\right ) \right \} \\
&=-\left ( \mathbf{a}, \mathbf{u}_i \right ) + \sum_{k=1}^{n} c_k \left (\mathbf{u}_k, \mathbf{u}_i \right )
\end{align}
\end{split}\]
関数の直交
離散データとベクトルで直交を定義し,正規方程式からの最小二乗法を導出したのと同様に関数に対しても直交を定義することができる.
区間\([a,b]\)で関数\(f(x), g(x)\)が以下のとき関数が直交するという.
\[
\int_{a}^{b}\ f(x) g(x) dx= 0
\]
そして,関数の集合 \(\{\phi_i(x)\}^n_{i=0}\) が互いに直交するとき,区間 \([a,b]\) 上の直交関数系であるという.
\[
\int_{a}^{b}\ \phi_{i}\left(x\right) \phi_{j}\left(x\right) dx= 0, \qquad i \neq j
\]
この関数の直交性を利用してベクトルと同様に関数の最小二乗法を考えることもできる.
以下に関数の最小二乗法についてまとめた.クリックすると確認できる.
関数の最小二乗法と直交性
区間 \([a,b]\) において,任意の関数 \(f(x)\) を\(n\) 個の関数 \(\{ \phi_i(x) \}^n_{i=1}\) の線形結合
\[\begin{split}
\begin{align}
f(x) &\approx \sum_{k=1}^{n} c_{k} \phi_{k}(x)\\
&=c_1 \phi_{1}(x)+c_2 \phi_{2}(x) + \cdots c_n \phi_n(x)
\end{align}
\end{split}\]
で表現する.ベクトルの場合と同様に,区間 \([a,b]\) 上のすべての点 \(x\) で均一に近似するように次の最小化問題を考える.
\[
J = \frac{1}{2} \int_{a}^{b} \left ( f \left ( x \right ) - \sum_{n}^{k=1} c_{k} \phi_{k}\left ( x \right ) \right ) ^ 2 dx \rightarrow min
\]
同じく,関数 \(J\) についてその偏導関数が \(0\) となるように係数 \(\{ c_i \}^n_{i=1}\) を求める.偏導関数は以下であり,
\[\begin{split}
\begin{align}
\frac{\partial J}{\partial c_i} &= -\int_{a}^{b} \left(f \left ( x \right ) - \sum_{k=1}^{n} c_{k} \phi_{k} \left(x \right) \right) \phi_{i} \left( x \right) dx \\
&= \sum_{k=1}^{n} c_k \int_{a}^{b} \phi_k \left ( x \right ) \phi_i \left ( x \right ) dx
- \int_{a}^{b} f \left ( x \right ) \phi_i \left ( x \right ) dx\\
\end{align}
\end{split}\]
正規方程式は以下のように定まる.
\[\begin{split}
\begin{pmatrix}
\int_{a}^{b} \phi_{1} \left ( x \right ) ^2 dx &
\int_{a}^{b} \phi_{1} \left ( x \right ) \phi_{2} \left ( x \right ) dx &
\cdots &
\int_{a}^{b} \phi_{1} \left ( x \right ) \phi_{n} \left ( x \right ) dx \\
\int_{a}^{b} \phi_{2} \left ( x \right ) \phi_{1} \left ( x \right ) dx &
\int_{a}^{b} \phi_{2} \left ( x \right ) ^2 dx &
\cdots &
\int_{a}^{b} \phi_{2} \left ( x \right ) \phi_{n} \left ( x \right ) dx \\
\vdots & \vdots & \ddots & \vdots \\
\int_{a}^{b} \phi_{n} \left ( x \right ) \phi_{1} \left ( x \right ) dx &
\int_{a}^{b} \phi_{n} \left ( x \right ) \phi_{2} \left ( x \right ) dx &
\cdots &
\int_{a}^{b} \phi_{n} \left ( x \right ) ^2 dx
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\int_{a}^{b} \phi_{1} \left ( x \right ) f \left ( x \right ) dx \\
\int_{a}^{b} \phi_{2} \left ( x \right ) f \left ( x \right ) dx \\
\vdots \\
\int_{a}^{b} \phi_{n} \left ( x \right ) f \left ( x \right ) dx
\end{pmatrix}
\end{split}\]
前述した関数の直交性より直交関数系 \(\{ \phi_{i}(x) \}^{n}_{i=1}\) を設計すると,関数の場合も,正規方程式の非対角成分は \(0\) となり,
\[\begin{split}
\begin{pmatrix}
\int_{a}^{b} \phi_{1} \left ( x \right )^2 dx &
&
&
\\
&
\int_{a}^{b} \phi_{2} \left ( x \right )^2 dx &
&
\\
&& \ddots &\\
&
&
&
\int_{a}^{b} \phi_{n} \left ( x \right )^2 dx
\end{pmatrix}
\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}
=
\begin{pmatrix}
\int_{a}^{b} \phi_{1} \left ( x \right ) f \left ( x \right ) dx \\
\int_{a}^{b} \phi_{2} \left ( x \right ) f \left ( x \right ) dx \\
\vdots \\
\int_{a}^{b} \phi_{n} \left ( x \right ) f \left ( x \right ) dx
\end{pmatrix}
\end{split}\]
各係数は簡単に計算できる.
\[
c_i = \frac{\int_{a}^{b} \phi_{i} \left ( x \right ) f \left ( x \right) dx }{\int_{a}^{b} \phi_{i} \left ( x \right )^2 dx }, \qquad i=1,...,n
\]
偏導関数の導出
\(\partial J / \partial c_i\)の式変形についてまとめたので参考にされたい.
\[\begin{split}
\begin{align}
\frac{\partial J}{\partial c_i} &= -\int_{a}^{b} \left(f \left ( x \right ) - \sum_{k=1}^{n} c_{k} \phi_{k} \left(x \right) \right) \phi_{i} \left( x \right) dx \\
&=-\int_{a}^{b} f \left ( x \right ) \phi_{i} \left( x \right) dx + \int_{a}^{b} \sum_{k=1}^{n} c_{k} \phi_{k} \left(x \right) \phi_{i} \left( x \right) dx \\
&= \sum_{k=1}^{n} \int_{a}^{b} c_k \phi_k \left ( x \right ) \phi_i \left ( x \right ) dx
- \int_{a}^{b} f \left ( x \right ) \phi_i \left ( x \right ) dx\\
&= \sum_{k=1}^{n} c_k \int_{a}^{b} \phi_k \left ( x \right ) \phi_i \left ( x \right ) dx
- \int_{a}^{b} f \left ( x \right ) \phi_i \left ( x \right ) dx\\
\end{align}
\end{split}\]


