Physics Informed Neural Network

解析的に解ける微分方程式は一部であり，大半の微分方程式は有限回の積分と変形で解けない微分方程式であった．このような解析的に解けない微分方程式は数値計算のアルゴリズムを用いて解が計算されるが，一般的に膨大な計算リソースを必要とする．この問題への解決への糸口として，常微分方程式や偏微分方程式で記述される物理法則の近似解を予測するニューラルネットワークである Physics Informed Neural Network（PINN） が注目を集めている．PINNsは求めたい関数 \(f\) の入出力関係 \(y=f(x)\) を 多層パーセプトロン（Multi Layer Perceptron; MLPs） でモデル化し，与えれた微分方程式・初期条件・境界条件から定義される誤差関数の最小化問題から関数 \(f\) を学習する．

PINNsによる熱伝導方程式の解の計算

熱伝導方程式の解をPINNsで学習する．熱伝導方程式は均質の物質で構成されている長さ \(L\) の棒について，時刻 \(t\) における位置 \(x\) の温度分布 \(u(x,t)\) を記述する偏微分方程式であった．熱伝導方程式（拡散方程式）は以下の式で与えられた．

\[ \frac{\partial u}{\partial t} = a^2 \frac{\partial^2 u}{\partial x^2}, a>0 \]

また棒の両端（定義域の端）の温度分布の制約として次の境界条件を設定する．

\[ u(0,t)=u(L,t)=0 \]

また時刻 \(t=0\) の温度分布として初期条件は以下で考える．

\[ u(x,0) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right) \]

この方程式は変数分離の仮定とフーリエ級数展開の利用から特殊解を導出できるが，ここではこの微分方程式の解をMLPsでモデル化したPINNsで学習する．

ライブラリのインポート

まずはじめに必要なライブラリをインポートする．今回は Numpy と Matplotlib に加えて PyTorch と呼ばれる深層学習ライブラリを利用する．

import torch
import matplotlib.pyplot as plt
import numpy as np

また今回利用した PyTorch のバージョンは以下である．

torch.__version__

'1.13.1'

データの作成

まず学習データ，境界条件，初期条件，プロット用のデータを作成する．各データはNumpyで一様分布に従ってランダム生成し，Pytorchで計算できるようにtorch.tensor を使って Tensor型へ変換する．

# パラメータ
L = 2.0
N, N_bc, N_ic = 1000, 100, 100

# 学習データ
N = 1000
x = torch.tensor(
    np.random.uniform(0, L, (N, 1)), dtype=torch.float32, requires_grad=True)
t = torch.tensor(
    np.random.uniform(0, 1, (N, 1)), dtype=torch.float32, requires_grad=True)

# 境界条件
N_bc = 100
x_bc = torch.tensor([0, L], dtype=torch.float32).view(-1, 1)
t_bc = torch.tensor([0, 0], dtype=torch.float32).view(-1, 1)

# 初期条件
N_ic = 100
x_ic = torch.tensor(np.random.uniform(0, L, (N_ic, 1)), dtype=torch.float32)
t_ic = torch.tensor([0]*N_ic, dtype=torch.float32).view(-1, 1)
u_ic = (1. / torch.sqrt(torch.tensor(2*np.pi*0.1))) * torch.exp(-(x_ic-1)**2 / (2*0.1))

# プロット用のデータ
N_plot = 100
xx_plot, tt_plot = np.meshgrid(
    np.linspace(0, L, N_plot), np.linspace(0, 1, N_plot))
xx_plot = torch.tensor(xx_plot.reshape(-1, 1), dtype=torch.float32)
tt_plot = torch.tensor(tt_plot.reshape(-1, 1), dtype=torch.float32)

各データの形状は .shape でみたときに (データ数, データの次元)となるように view メソッドを使って整形している．

x.shape, t.shape

(torch.Size([1000, 1]), torch.Size([1000, 1]))

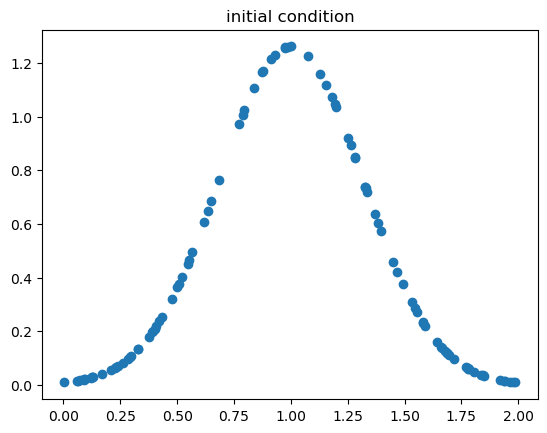
実際の関数の出力結果の値が定義されているのは初期条件のデータのみに注意されたい．そのため今回考える初期条件を可視化しておく．

plt.scatter(x_ic.numpy(), u_ic.numpy())
plt.title('initial condition')

Text(0.5, 1.0, 'initial condition')

PINNsの定義

続いて変数 \(x,t\) を入力とし解 \(u(x,t)\) を出力するニューラルネットワークを構築する．Pytorchでは torch.nn.Module を継承したクラスを用いてニューラルネットワークを定義する．簡単に解説すると，__init__ メソッド内で線形変換を行う 全結合層 torch.nn.Linear を3層定義している．全結合層の引数はそれぞれ入力次元, 出力次元を表す．

forward メソッドはニューラルネットワークの 順伝播（forward propagation） を定義する．メソッドの引数は関数への入力 \(x,t\) を与え，モデル化した関数の出力 \(y\) を返す．forward ではまず cat 関数で x と t の値を結合し，定義した全結合層に伝播している．各全結合層の出力は tanh関数（Hyperbolic tangent function; 双曲線正接関数） によって非線形変換される．

class PINN(torch.nn.Module):
    def __init__(self, input_dim=2, hidden_dim=32, output_dim=1):
        super(PINN, self).__init__()
        self.fc1 = torch.nn.Linear(input_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = torch.nn.Linear(hidden_dim, output_dim)

    def forward(self, x, t):
        inputs = torch.cat([x, t], dim=1)
        h = torch.tanh(self.fc1(inputs))
        h = torch.tanh(self.fc2(h))
        y = self.fc3(h)
        return y

構築したニューラルネットワークをインスタンス化する．

f = PINN()
optimizer = torch.optim.Adam(f.parameters(), lr=0.01)

PINNsの誤差関数

では，与えられた熱伝導方程式解くために，偏微分方程式に関する誤差（pde_loss），初期条件に関する誤差（ic_loss），境界条件に関する誤差（bc_loss）を次のように定義する．torch.autograd.grad で引数として与えた outputs を inputs で微分したときの値を計算できる．そのため，u_t と u_x はそれぞれ \(u(x,t)\) の \(x\) と \(t\) に関する一階微分を表す．一方で u_xx は \(x\) の二階微分を表す．

pde_loss は与えられた微分方程式に関する誤差である．セル内の pde_loss = torch.mean((u_t - alpha * u_xx)**2) が対応している．これの式の意味は与えられた微分方程式

\[ \frac{\partial u}{\partial t} - a^2 \frac{\partial^2 u}{\partial x^2} = 0 \]

の右辺が左辺と等しくなるように，つまり右辺が \(0\) になるような平均二乗誤差を示している．

def calc_pde_loss(f, x, t, alpha):
    u = f(x, t)
    u_t = torch.autograd.grad(outputs=u, inputs=t, 
                              grad_outputs=torch.ones_like(u), create_graph=True)[0]
    u_x = torch.autograd.grad(outputs=u, inputs=x, 
                              grad_outputs=torch.ones_like(u), create_graph=True)[0]
    u_xx = torch.autograd.grad(outputs=u_x, inputs=x, 
                               grad_outputs=torch.ones_like(u_x), create_graph=True)[0]
    pde_loss = torch.mean((u_t - alpha * u_xx)**2)
    return pde_loss

初期条件の誤差 ic_loss は同様に初期条件と予測結果が一致するとき最小の値をとる平均二乗誤差を表す．

def calc_ic_loss(f, x_ic, t_ic, u_ic):
    u_ic_pred = f(x_ic, t_ic)
    ic_loss = torch.mean((u_ic - u_ic_pred)**2)
    return ic_loss

境界条件についても同様である．

def calc_bc_loss(f, x_bc, t_bc):
    u_bc_pred = f(x_bc, t_bc)
    bc_loss = torch.mean(u_bc_pred**2)
    return bc_loss

PINNsの学習

続いて，定義したPINNsを定義した誤差が最小になるように 最急降下法（Gradient Descent） で学習する．最急降下法は与えられたパラメータ \(\theta\) を持つモデル \(f\) （今回はMLPs）について誤差の 勾配（Gradient） を計算し，勾配の逆方向にパラメータを更新することで，誤差関数を最小化するパラメータを求めるアルゴリズムである．最急降下法は基本的には，パラメータの初期化（optimizer.zero_grad()），誤差関数の値を計算（loss = pde_loss + ic_loss + bc_loss），勾配を計算（loss.backward()），パラメータの更新（optimizer.step()）の4ステップからなる．ここで現れる optimizer はモデルのパラメータを管理・更新するためのクラスのようなものである．

このステップを N_iter 回繰り返す．以下が実装である．

alpha = 0.1
N_iter = 3000
for i in range(N_iter):
    optimizer.zero_grad()
    
    pde_loss = calc_pde_loss(f, x, t, alpha)
    ic_loss = calc_ic_loss(f, x_ic, t_ic, u_ic)
    bc_loss = calc_bc_loss(f, x_bc, t_bc)

    loss = pde_loss + ic_loss + bc_loss
    
    loss.backward()
    optimizer.step()

    if i % 100 == 0:
        print(f"Iteration {i}, Loss {loss.item()}")

Iteration 0, Loss 0.4656802713871002

Iteration 100, Loss 0.02137128822505474

Iteration 200, Loss 0.0036200066097080708

Iteration 300, Loss 0.0011011644965037704

Iteration 400, Loss 0.0002914892102126032

Iteration 500, Loss 0.00019304353918414563

Iteration 600, Loss 0.0007867459789849818

Iteration 700, Loss 8.529241313226521e-05

Iteration 800, Loss 6.70115405227989e-05

Iteration 900, Loss 0.0020131126511842012

Iteration 1000, Loss 4.368781446828507e-05

Iteration 1100, Loss 0.000651445472612977

Iteration 1200, Loss 3.473555261734873e-05

Iteration 1300, Loss 2.906210283981636e-05

Iteration 1400, Loss 0.0010433680145069957

Iteration 1500, Loss 2.4170944016077556e-05

Iteration 1600, Loss 8.797281770966947e-05

Iteration 1700, Loss 2.2287078536464833e-05

Iteration 1800, Loss 1.98054713109741e-05

Iteration 1900, Loss 2.9732120310654864e-05

Iteration 2000, Loss 1.9959099518018775e-05

Iteration 2100, Loss 1.7663376638665795e-05

Iteration 2200, Loss 0.00013659719843417406

Iteration 2300, Loss 1.691353645583149e-05

Iteration 2400, Loss 1.5464922398678027e-05

Iteration 2500, Loss 0.00010546203702688217

Iteration 2600, Loss 1.56636415340472e-05

Iteration 2700, Loss 1.5103287296369672e-05

Iteration 2800, Loss 1.6334384781657718e-05

Iteration 2900, Loss 1.444278041162761e-05

誤差の値をprintしてみてもわかるように誤差関数の値が減少し，熱伝導方程式とその条件をうまく学習できていることがわかる．

PINNsの出力の可視化

最後に学習されたPINNsの出力結果を確認する．基本的には第13回でのプロットと同じであるが，勾配を計算しないように with torch.no_grad() を呼び出していることに注意されたい．このスケールのニューラルの学習では無視できるが大きなニューラルネットワークを学習するときに勾配計算は非常に重く，メモリを要する処理である．torch.no_grad() は勾配計算をしないようにする処理である．

with torch.no_grad():
    u_pred = f(xx_plot, tt_plot)
    u_pred = u_pred.reshape(N_plot, N_plot).numpy()
    plt.imshow(u_pred, cmap='magma')
    plt.axis('off')
    plt.title(f'Iteration {N_iter}')

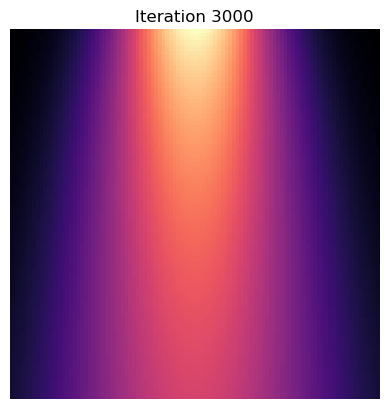
結果をみると熱の広がりを表す解が学習から獲得できていることがわかる．以上より，PINNsと呼ばれるニューラルネットワークを用いて熱伝導方程式の解を学習から発見することができた．