ホイン法

ホイン法（Heun’s method） または 改良オイラー法（Improved Euler’s method） はオイラー法で利用する始点 \(t\) での関数の傾きの代わりに，始点 \(t\) と終点 \(t+h\) での傾きの平均を用いて近似を行う．つまり，

\[ \begin{aligned} x(t+h) = x(t) + \frac{h}{2} \left \{ f\left (x \left (t \right),t\right)+ f\left (x + hf\left(x,t\right),t + h\right)\right \} \end{aligned} \]

の近似式を利用する．

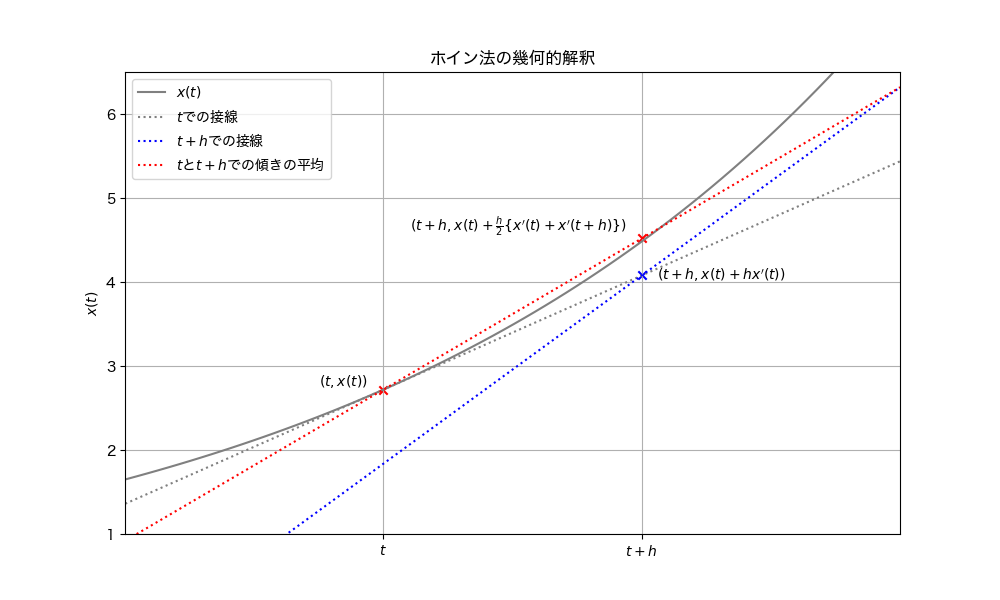
オイラー法と同様にこの近似式の幾何的解釈を図に示す．ホイン法では始点 \(t\) での傾き（図の灰色の点線）に加えて，終点 \(t+h\) での傾き（図の青色の点線）の情報を利用する．近似式からもわかるように，これらの傾きを平均した傾きを使って次の時刻 \(t+h\) での関数の値を外挿する（図の赤色の点線）．これを数値列の近似として書くと，

\[\begin{split} \begin{aligned} \tilde{x}_{i+1} &= x_i + hf\left(x_i,t_i \right) \\ x_{i+1} &= x_i + \frac{h}{2} \left \{ f\left(x_i,t_i \right) + f\left(\tilde{x}_{i+1},t_{i+1} \right)\right \} \end{aligned} \end{split}\]

となる．ホイン法は二次の精度をもつ近似法として知られている．このことは次のようにオイラー法から修正した導関数，つまり，次の時刻の関数の値 \(f(x+hf(x,t),t+h)\) のTaylor展開をすることで確認できる．二変数関数であることに注意すると

\[ \begin{aligned} f(x+hf(x,t), t+h) = f(x,t)+h \frac{\partial f}{\partial t} + h\frac{\partial f}{\partial x} \frac{dx}{dt} +O(h^2) \end{aligned} \]

となる．続いて，これをホイン法で用いた近似式に代入する．

\[\begin{split} \begin{aligned} x(t+h) &= x(t) + \frac{h}{2} \left \{ f\left (x \left (t \right),t\right)+ f\left (x\left(t\right) + hf\left(x,t\right),t + h\right)\right \} \\ &= x(t) + \frac{h}{2} \left \{ f\left (x \left (t \right),t\right)+ f(x(t),t)+h \frac{\partial f}{\partial t} + h\frac{\partial f}{\partial x} \frac{dx}{dt}+O(h^2)\right \} \\ &= x(t) + h f\left (x \left (t \right),t\right) + \frac{h^2}{2} \left \{ \frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} \frac{dx}{dt} \right \} + O(h^3) \\ &= x(t) + h x'(t) + \frac{h^2}{2} x''(t) + O(h^3) \end{aligned} \end{split}\]

ここで \(f(x(t),t)=x'(t)\) であり，\(x(t)\) の二階導関数が

\[ \begin{aligned} x''(t)=\frac{d^2 x}{d t^2}=\frac{\partial f}{\partial t}+\frac{\partial f}{\partial x} \frac{d x}{d t} \end{aligned} \]

であることを利用した．式からもわかるように右辺第3項まで \(x(t+h)\) のTaylor展開と一致しており，ホイン法が二階の導関数までを含む二次近似をしており，オイラー法より優れたアルゴリズムであることがわかる．

ホイン法の実装

これをPythonで実装する．今回は次の初期値問題を解く

\[ x'=x(1-x), x(0)=\frac{1}{2} \]

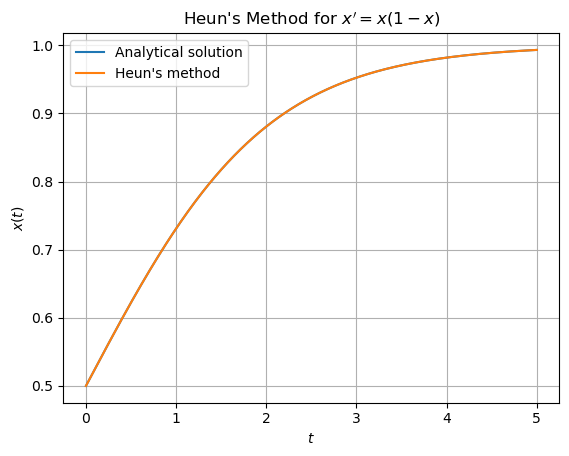
解答：解析解は \(x=\frac{1}{1+e^{-t}}\) であり，以下のプログラムで解析解と近似解の違いをプロットする．

import numpy as np
import matplotlib.pyplot as plt

def heun_method(f, x0, t0, tn, h):
    """
    ホイン法（修正オイラー法）を用いて常微分方程式を数値的に解く関数
    :param f: 常微分方程式の右辺の関数 f(t, x) 
    :param x0: 初期値 x(t0)
    :param t0: 初期時刻
    :param tn: 最終時刻
    :param h: 刻み幅
    :return: 時刻と近似解のリスト
    """
    t_values = [t0] # t_0の値を格納したリストを作成
    x_values = [x0] # x_0の値（初期値）を格納したリストを作成
    
    t = t0
    x = x0
    
    while t < tn: # 最終時刻になるまで繰り返す
        # 時刻と式()に基づく値の更新
        k1 = h * f(t, x)
        k2 = h * f(t + h, x + k1)
        x = x + 0.5 * (k1 + k2)
        t = t + h
        
        # 計算された値をリストに追加
        t_values.append(t)
        x_values.append(x)
        
    return t_values, x_values

# 微分方程式の右辺
def f(t, x):
    return x * (1 - x)

# 解析解
def analytical_solution(t):
    return 1. / (1 + np.exp(-t))

# 初期値とパラメータ
x0 = 0.5 # 初期値
t0 = 0 # 開始時刻
tn = 5 # 終了時刻
h = 0.001 # 刻み幅

plt.figure()
t_analytical = np.linspace(t0, tn, 500) # 区間[開始時刻,終了時刻]で時刻を500点サンプリング
x_analytical = analytical_solution(t_analytical) # 解析解の計算
plt.plot(t_analytical, x_analytical, label='Analytical solution') # 解析解のプロット 

t_values, x_values = heun_method(f, x0, t0, tn, h) # ホイン法の計算
plt.plot(t_values, x_values, label="Heun's method") # ホイン法の結果のプロット
plt.title(r"Heun's Method for $x' = x(1-x)$")
plt.xlabel(r'$t$')
plt.ylabel(r'$x(t)$')
plt.grid(True)
plt.legend()
plt.show()